某人从甲地去乙地共走了500m.途经一条宽为x m的河流.该人不小心把一件物品丢在途中.若物品掉在河里就找不到.若物品不掉在河里就能找到．已知该物品能被找到的概率为$\frac{24}{25}$.则河宽为( )A．80mB．20mC．40mD．50m 题目和参考答案——青夏教育精英家教网—

题目内容

9．某人从甲地去乙地共走了500m，途经一条宽为x m的河流，该人不小心把一件物品丢在途中，若物品掉在河里就找不到，若物品不掉在河里就能找到．已知该物品能被找到的概率为$\frac{24}{25}$，则河宽为（　　）

A．

80m

B．

20m

C．

40m

D．

50m

分析本题考查的知识点是几何概型的意义，关键是要找出找到该物品的点对应的图形的长度，并将其和整个事件的长度代入几何概型计算公式进行求解．

解答解：由已知易得：
l_{从甲地到乙}=500
l_途中涉水=x，
故物品遗落在河里的概率P=$\frac{x}{500}=1-\frac{24}{25}$，
∴x=20（m）．
故

点评本题考查的知识点是几何概型的意义，几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．

练习册系列答案

6．给出下列四个命题：
①“三个球全部放入两个盒子，其中必有一个盒子有一个以上的球”是必然事件
②“当x为某一实数时可使x²＜0”是不可能事件
③“明天广州要下雨”是必然事件
④“从100个灯泡中有5个次品，从中取出5个，5个都是次品”是随机事件，
其中正确命题的个数是（　　）

3．设集合A={x|（x-1）（x-2）＜0}，集合B={x|1＜x＜3}，则A∪B=（　　）

4．已知F₁，F₂为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，O是坐标原点，过F₂作垂直于x轴的直线MF₂交椭圆于M（$\sqrt{2}$，1）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过左焦点F₁的直线l与椭圆C交于A、B两点，若$\overrightarrow{OA}$•$\overrightarrow{OB}$=0，求直线l的方程．

14．

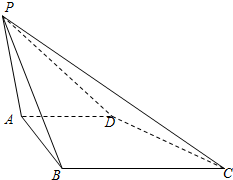如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，侧面PAD同时垂直侧面PAB与侧面PDC．若PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB，则$\frac{BC}{AD}$=$\frac{3}{2}$，直线PC与底面ABCD所成角的正切值为$\frac{\sqrt{6}}{6}$．

1．直线2x-2y+1=0的倾斜角是（　　）

18．若x＞0，则函数y=x+$\frac{1}{2x+1}$的最小值为$\sqrt{2}-\frac{1}{2}$．

19．设向量$\overrightarrow{a}$、$\overrightarrow{b}$满足：|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，$\overrightarrow{a}$•$\overrightarrow{b}$=1，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是（　　）

试题分类