题目内容
3.二项式($\frac{x}{\sqrt{2}}$-y)8的展开式中,x4y4与x2y6项的系数之和是$\frac{63}{2}$(用数字作答)分析 根据二项式展开式的通项公式,求出x4y4与x2y6项的系数,再求和即可.
解答 解:($\frac{x}{\sqrt{2}}$-y)8的展开式中,通项公式为
Tr+1=${C}_{8}^{r}$•${(\frac{x}{\sqrt{2}})}^{8-r}$•(-y)r=$\frac{{(-1)}^{r}}{{(\sqrt{2})}^{8-r}}$•x8-r•yr,
当r=4时,可得x4y4的系数为$\frac{{(-1)}^{4}}{{(\sqrt{2})}^{8-4}}$•${C}_{8}^{4}$=$\frac{35}{2}$;
当r=6时,可得x2y6的系数为$\frac{{(-1)}^{6}}{{(\sqrt{2})}^{8-6}}$•${C}_{8}^{6}$=14;
所以展开式中x4y4与x2y6项的系数之和是$\frac{35}{2}$+14=$\frac{63}{2}$.
故答案为:$\frac{63}{2}$
点评 本题考查了二项式展开式的通项公式的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.在△ABC中,已知角A、B、C所对的边分别为a,b,c.已知A=$\frac{π}{3}$,a=$\sqrt{3}$,b=2.则B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
16.设椭圆C:y2+$\frac{{x}^{2}}{{m}^{2}}$=1(0<m<1)的两焦点分别为F1,F2,若在椭圆C上存在点P使得PF1⊥PF2,则m的取值范围是( )
| A. | [$\frac{\sqrt{2}}{2}$,1) | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{1}{2}$,1) | D. | (0,$\frac{1}{2}$] |
8.执行如图所示的程序框图,输出S的值为$\frac{1}{2}$时,k是( )
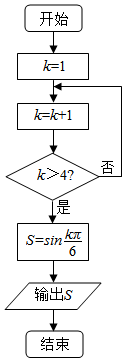

| A. | 5 | B. | 3 | C. | 4 | D. | 2 |
15.已知函数f(x)=$\left\{{\begin{array}{l}{3+{{log}_2}x,x>0}\\{{x^2}-x-1,x≤0}\end{array}}$,则不等式f(x)≤5的解集为( )
| A. | [-1,1] | B. | (-∞,-2]∪(0,4) | C. | [-2,4] | D. | (-∞,-2]∪[0,4] |