题目内容
20.已知f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,则满足f(a)-f(-a)<1的a的取值范围是( )| A. | (-∞,3) | B. | (-∞,log23) | C. | (3,+∞) | D. | (log23,+∞) |
分析 根据函数f(x)的解析式,化简不等式f(a)-f(-a)<1,求出解集即可.
解答 解:∵f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,
∴f(a)-f(-a)<1,
即$\frac{{2}^{a}-1}{{2}^{a}+1}$-$\frac{{2}^{-a}-1}{{2}^{-a}+1}$<1,
化简得$\frac{{2}^{a}-1}{{2}^{a}+1}$<$\frac{1}{2}$,
即$\frac{1}{{2}^{a}+1}$>$\frac{1}{4}$,
∴2a+1<4,
即2a<3,
解得a<log23,
∴a的取值范围是(-∞,log23).
故选:B.
点评 本题考查了指数函数的图象与性质的应用问题,也考查了解不等式的应用问题,是基础题目.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.在△ABC中,已知角A、B、C所对的边分别为a,b,c.已知A=$\frac{π}{3}$,a=$\sqrt{3}$,b=2.则B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
8.执行如图所示的程序框图,输出S的值为$\frac{1}{2}$时,k是( )
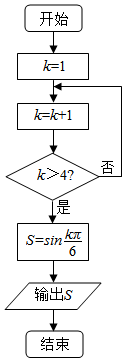

| A. | 5 | B. | 3 | C. | 4 | D. | 2 |