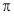题目内容
6.函数f(x)=(1+$\sqrt{3}$tan2x)cos2x的最小正周期为( )| A. | 2π | B. | $\frac{3π}{2}$ | C. | π | D. | $\frac{π}{2}$ |
分析 根据三角函数的辅助角公式进行化简,结合三角函数的周期公式进行求解即可.
解答 解:f(x)=(1+$\sqrt{3}$tan2x)cos2x=(1+$\sqrt{3}$•$\frac{sin2x}{cos2x}$)cos2x=cos2x+$\sqrt{3}$sin2x=2cos(2x-$\frac{π}{6}$),
则函数的周期T=$\frac{2π}{2}$=π,
故选:C
点评 本题主要考查三角函数周期的计算,根据三角函数的辅助角公式进行化简是解决本题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
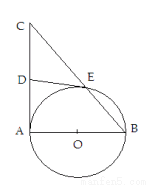
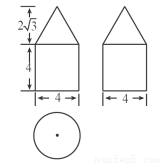
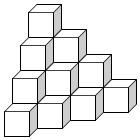 如图所示,若每个小正方体的棱长为1cm.求
如图所示,若每个小正方体的棱长为1cm.求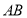 是
是 的直径,
的直径,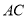 是
是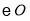 的切线,
的切线, 交
交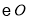 于点
于点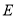 .
.
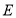 做
做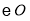 的切线,交
的切线,交 ,证明:
,证明: 是
是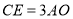 ,求
,求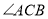 的大小.
的大小. ( )
( ) B.
B. C.
C. D.
D.
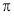 B.24
B.24 C.28
C.28 D.32
D.32