题目内容
9.已知正三角形ABC内接于半径为2的圆O,点P是圆O上的一个动点,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围是[-2,6].分析 建立坐标系,设P(2cosθ,sinθ),求出$\overrightarrow{PA},\overrightarrow{PB}$的坐标,代入数量积公式得到关于θ的三角函数,利用正弦函数的性质得出.
解答  解:以三角形的外接圆圆心为原点建立平面直角坐标系.
解:以三角形的外接圆圆心为原点建立平面直角坐标系.
设A(2,0),B(-1,$\sqrt{3}$),P(2cosθ,2sinθ).
则$\overrightarrow{PA}$=(2cosθ-2,2sinθ),$\overrightarrow{PB}$=(2cosθ+1,2sinθ-$\sqrt{3}$).
∴$\overrightarrow{PA}•\overrightarrow{PB}$=(2cosθ-2)(2cosθ+1)+2sinθ(2sinθ-$\sqrt{3}$)
=2-2cosθ-2$\sqrt{3}$sinθ
=2-4sin(θ+$\frac{π}{6}$).
∴-2≤$\overrightarrow{PA}•\overrightarrow{PB}$≤6.
故答案为[-2,6].
点评 本题考查了平面向量的数量积运算,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
19.若|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=5,$\overrightarrow{a}$$•\overrightarrow{b}$=5$\sqrt{3}$,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角θ=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
20.已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,Sn是{an}的前n项和,则S9等于( )
| A. | -8 | B. | -6 | C. | 10 | D. | 0 |
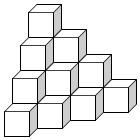 如图所示,若每个小正方体的棱长为1cm.求
如图所示,若每个小正方体的棱长为1cm.求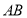 是
是 的直径,
的直径,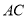 是
是 的切线,
的切线, 交
交 于点
于点 .
.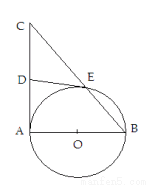
 做
做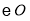 的切线,交
的切线,交 ,证明:
,证明: 是
是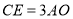 ,求
,求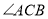 的大小.
的大小. 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.