题目内容
已知椭圆E: 过点
过点 ,且离心率为
,且离心率为 .
.
(1)求椭圆E的方程;
(2)设直线 交椭圆E于A,B两点,判断点G
交椭圆E于A,B两点,判断点G
与以线段AB为直径的圆的位置关系,并说明理由.
 |
解法一:(1)由已知得

所以椭圆E的方程为 .
.
(2)设点 AB中点为
AB中点为 .
.
由
所以 从而
从而 .
.
所以 .
.

 ,
,
故
所以 ,故G
,故G 在以AB为直径的圆外.
在以AB为直径的圆外.
解法二:(1)同解法一.
(2)设点 ,则
,则
由 所以
所以
从而


所以 不共线,所以
不共线,所以 为锐角.
为锐角.
故点G 在以AB为直径的圆外.
在以AB为直径的圆外.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
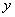 (单位:小时)与储藏温度
(单位:小时)与储藏温度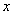 (单位:℃)满足函数关系
(单位:℃)满足函数关系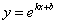 (
(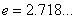 为自然对数的底数,
为自然对数的底数,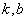 为常数)。若该食品在
为常数)。若该食品在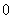 ℃的保鲜时间是
℃的保鲜时间是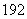 小时,在
小时,在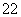 ℃的保鲜时间是
℃的保鲜时间是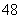 小时,则该食品在
小时,则该食品在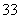 ℃的保鲜时间是
℃的保鲜时间是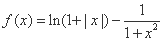 ,则使得
,则使得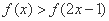 成立的
成立的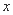 的取值范围是
的取值范围是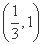 B.
B. C.
C.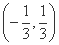 D.
D.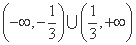

 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,函数
,函数 ,若在矩形
,若在矩形 内随机取一点,则此点取自阴影部分的概率等于 .
内随机取一点,则此点取自阴影部分的概率等于 .
 的最小值为4.
的最小值为4. 的值;
的值; 的最小值为.
的最小值为. =
= (B)8 (C)4
(B)8 (C)4

 与圆
与圆
 相交于不同的两点
相交于不同的两点 ,
, .
. 求圆
求圆 的圆心坐标;
的圆心坐标; 求线段
求线段 的中点
的中点 的轨迹
的轨迹 的方程;
的方程; 是否存在实数
是否存在实数 ,使得直线
,使得直线
 与曲线
与曲线