题目内容
6. 如图,直三棱柱ABC-A1B1C1中,AB=BC,AC=AA1=2$\sqrt{2}$,E为A1C上一点,且A1C=4EC,F为AC的中点.
如图,直三棱柱ABC-A1B1C1中,AB=BC,AC=AA1=2$\sqrt{2}$,E为A1C上一点,且A1C=4EC,F为AC的中点.(1)证明:A1C⊥平面BEF;
(2)若平面A1BC⊥平面A1B1BA,求三棱柱ABC-A1B1C1的体积.
分析 (1)连结BF,由AA1⊥平面ABC得AA1⊥BF,通过计算CF,CE可发现$\frac{CF}{{A}_{1}C}$=$\frac{CE}{AC}$=$\frac{\sqrt{2}}{4}$,故△CEF∽△CAA1,故∠CEF=∠CAA1=90°,故A1C⊥EF,于是A1C⊥平面BEF;
(2)由面面垂直的性质可得BC⊥平面A1B1BA,于是AB⊥BC,求出底面积即可求出棱柱的体积.
解答 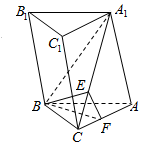 (1)证明连结BF,
(1)证明连结BF,
∵AA1⊥平面ABC,BF?平面ABC,
∴AA1⊥BF,
∵AB=BC,F是AC的中点,
∴AC⊥BF,
又AC?平面A1CA,A1A?平面A1CA,AC∩AA1=A,
∴BF⊥平面A1CA,∵A1C?平面A1CA,
∴BF⊥A1C.
∵AC=A1A=2$\sqrt{2}$,AC⊥A1A,F是AC的中点,A1C=4EC,
∴A1C=4,CF=$\sqrt{2}$,CE=1.
∴$\frac{CF}{{A}_{1}C}$=$\frac{CE}{AC}$=$\frac{\sqrt{2}}{4}$.
∴△CEF∽△CAA1,
∴A1C⊥EF,又EF?平面BEF,BF?平面BEF,EF∩BF=F,
∴A1C⊥平面BEF.
(2)∵平面A1BC⊥平面A1B1BA,平面ABC⊥平面A1B1BA,平面ABC∩平面A1BC=BC,
∴BC⊥平面A1B1BA,∵AB?平面A1B1BA,
∴BC⊥AB.又∵AC=2$\sqrt{2}$,AB=BC,
∴AB=BC=2.
∴三棱柱ABC-A1B1C1的体积V=S△ABC•AA1=$\frac{1}{2}×{2}^{2}×2\sqrt{2}$=4$\sqrt{2}$.
点评 本题考查了线面垂直的性质与判定,棱柱的体积计算,属于中档题.

练习册系列答案
相关题目
16.已知复数i•(1+ai)为纯虚数,那么实数a的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
1.袋子中装有大小相同的6个小球,2红1黑3白,现从中有放回的随机摸球2此,每次摸出1个小球,则2次摸球颜色不同的概率是( )
| A. | $\frac{5}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{11}{18}$ | D. | $\frac{13}{18}$ |
15.设函数f(x)对x≠0的实数满足f(x)-2f($\frac{1}{x}$)=3x+2,那么${∫}_{1}^{2}$f(x)dx=( )
| A. | -($\frac{7}{2}$+2ln2) | B. | $\frac{7}{2}$+2ln2 | C. | -($\frac{7}{2}$+ln2) | D. | -(4+2ln2) |