题目内容
1.已知数列{an}满足:${log_3}a{\;}_n+1={log_3}{a_{n+1}},({n∈{N^+}})$,且a2+a4+a6=9,则${log_{\frac{1}{3}}}({a_5}+{a_7}+{a_9})$的值为-5.分析 由已知数列递推式结合对数的运算性质可得数列{an}是公比为3的等比数列,由已知a2+a4+a6=9,结合等比数列的性质可得a5+a7+a9的值,代入${log_{\frac{1}{3}}}({a_5}+{a_7}+{a_9})$得答案.
解答 解:由${log_3}a{\;}_n+1={log_3}{a_{n+1}},({n∈{N^+}})$,得log3(3an)=log3an+1,
∴an+1=3an,且an>0,
∴数列{an}是公比为3的等比数列,
又a2+a4+a6=9,∴${a}_{5}+{a}_{7}+{a}_{9}=({a}_{2}+{a}_{4}+{a}_{6})•{q}^{3}$=35.
∴${log_{\frac{1}{3}}}({a_5}+{a_7}+{a_9})$=$lo{g}_{\frac{1}{3}}{3}^{5}=-5$.
故答案为:-5.
点评 本题考查数列递推式,考查了对数的运算性质,考查等比数列的性质,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.设x,y满足约束条件$\left\{{\begin{array}{l}{x,y≥0}\\{x-y≥-1}\\{x+y≤3}\end{array}}\right.$,则z=x-2y的最大值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13.下列函数中既是偶函数,又在(0,+∞)上单调递减的为( )
| A. | $y={x^{-\frac{1}{2}}}$ | B. | y=x-2 | C. | $y={x^{\frac{1}{2}}}$ | D. | y=x2 |
10.若偶函数f(x)在[1,+∞)上是减函数,则下列关系式中成立的是( )
| A. | $f(2)<f(-\frac{3}{2})<f(-1)$ | B. | $f(-\frac{3}{2})<f(-1)<f(2)$ | C. | $f(2)<f(-1)<f(-\frac{3}{2})$ | D. | $f(-1)<f(-\frac{3}{2})<f(2)$ |
11.抛物线y2=2x的准线方程是( )
| A. | y=-1 | B. | $y=-\frac{1}{2}$ | C. | x=-1 | D. | $x=-\frac{1}{2}$ |
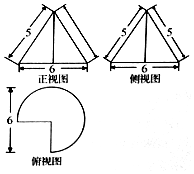 一个几何体的三视图如图所示,正视图和侧视图是两个全等的三角形,俯视图是$\frac{3}{4}$个圆,则该几何体的体积等于9π.
一个几何体的三视图如图所示,正视图和侧视图是两个全等的三角形,俯视图是$\frac{3}{4}$个圆,则该几何体的体积等于9π.