题目内容
某分公司有甲、乙、丙三个项目向总公司申报,总公司有Ⅰ、Ⅱ、Ⅲ三个部门进行评估审批,已知这三个部门的审批通过率分别为
、
、
.只要有两个部门通过就能立项,立项的每个项目能获得总公司100万的投资.
(1)求甲项目能立项的概率;
(2)设该分公司这次申报的三个项目获得的总投资额为X,求X的概率分布列及数学期望.
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
(1)求甲项目能立项的概率;
(2)设该分公司这次申报的三个项目获得的总投资额为X,求X的概率分布列及数学期望.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:应用题,概率与统计
分析:(1)设Ⅰ、Ⅱ、Ⅲ三个部门审批通过分别计为事件A,B,C,利用甲项目能立项的概率为:P=P(ABC+AB
+A
C+
BC),即可得出结论;
(2)X的可能取值为0,100,200,300,求出相应的概率,可得X的概率分布列及数学期望.
. |
| C |
. |
| B |
. |
| A |
(2)X的可能取值为0,100,200,300,求出相应的概率,可得X的概率分布列及数学期望.
解答:
解:(1)设Ⅰ、Ⅱ、Ⅲ三个部门审批通过分别计为事件A,B,C,
则P(A)=
,P(B)=
,P(C)=
.…(2分)
甲项目能立项的概率为:P=P(ABC+AB
+A
C+
BC)
=
×
×
+
×
×
+
×
×
+
×
×
=
∴甲项目能立项的概率为
; …(6分)
(2)X的可能取值为0,100,200,300. …(7分)
P(X=0)=
(
)3=
,P(X=100)=
×
×(
)2=
,
P(X=200)=
×(
)2×
=
,P(X=300)=
×(
)3=
,…(9分)
X的概率分布列为:
…(10分)
X的数学期望为EX=0×
+100×
+200×
+300×
=200(万).…(12分)
另解:设通过的项目数为变量m,则m~B(3,
),X=100m,EX=100×3×
=200万.
则P(A)=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
甲项目能立项的概率为:P=P(ABC+AB
. |
| C |
. |
| B |
. |
| A |
=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴甲项目能立项的概率为
| 2 |
| 3 |
(2)X的可能取值为0,100,200,300. …(7分)
P(X=0)=
| C | 0 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
P(X=200)=
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
X的概率分布列为:
| X | 0 | 100 | 200 | 300 | ||||||||
| P |
|
|
|
|
X的数学期望为EX=0×
| 1 |
| 27 |
| 2 |
| 9 |
| 4 |
| 9 |
| 8 |
| 27 |
另解:设通过的项目数为变量m,则m~B(3,
| 2 |
| 3 |
| 2 |
| 3 |
点评:熟练掌握相互独立事件的概率乘法公式、离散型随机变量的期望计算公式是解题的关键.

练习册系列答案
相关题目
 在三棱锥S-ABC中,O是AB的中点,SA=SB=
在三棱锥S-ABC中,O是AB的中点,SA=SB=

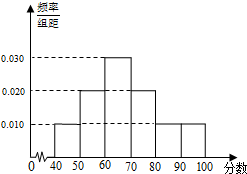 某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是
某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是