题目内容
在△ABC中,a+b=10,cosC是方程2x2+9x+4=0的一个根,求△ABC周长的最小值.
考点:正弦定理
专题:解三角形
分析:先由条件求得 cosC=-
,再由余弦定理可得 c2=(a-5)2+75,利用二次函数的性质求得c的最小值,即可求得△ABC周长a+b+c 的最小值.
| 1 |
| 2 |
解答:
解:解方程2x2+9x+4=0可得,
x=-4,或 x=-
.
∵cosC是方程2x2-3x-2=0的一个根,且|cosC|≤1,
∴cosC=-
.
由余弦定理可得
c2=a2+b2-2ab•cosC=(a+b)2-ab,
将b=10-a代入上式得,
∴c2=(a-5)2+75.
故当a=5时,c最小为
=5
,
故△ABC周长a+b+c 的最小值为 10+5
.
x=-4,或 x=-
| 1 |
| 2 |
∵cosC是方程2x2-3x-2=0的一个根,且|cosC|≤1,
∴cosC=-
| 1 |
| 2 |
由余弦定理可得
c2=a2+b2-2ab•cosC=(a+b)2-ab,
将b=10-a代入上式得,
∴c2=(a-5)2+75.
故当a=5时,c最小为
| 75 |
| 3 |
故△ABC周长a+b+c 的最小值为 10+5
| 3 |
点评:本题主要考查一元二次方程的解法、二次函数的性质以及余弦定理的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
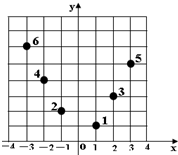 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示:
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示:| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A、501 | B、502 |
| C、503 | D、504 |
复数z=
的虚部为( )
| 2 |
| -1+i |
| A、-1 | B、-i | C、1 | D、i |