题目内容
12.如果复数z=a2-a-2+(a+1)i为纯虚数,那么实数a的值为2.分析 由实部为0且虚部不为0列式求得a值.
解答 解:∵复数z=a2-a-2+(a+1)i为纯虚数,
∴$\left\{\begin{array}{l}{{a}^{2}-a-2=0}\\{a+1≠0}\end{array}\right.$,解得a=2.
故答案为:2.
点评 本题考查复数的基本概念,是基础的计算题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知集合A={x|2x>1},B={x|x2-2x-3<0},则A∩B=( )
| A. | (-1,0) | B. | (0,1) | C. | (0,3) | D. | (1,3) |
20.已知函数f(x)=$\left\{\begin{array}{l}lnx,x>1\\ \frac{1}{4}x+1,x≤1\end{array}$,g(x)=ax,则方程g(x)=f(x)恰有两个不同的实根时,实数a的取值范围是( )(注:e为自然对数的底数)
| A. | $({0,\frac{1}{e}})$ | B. | $[{\frac{1}{4},\frac{1}{e}})$ | C. | $({0,\frac{1}{4}}]$ | D. | $({\frac{1}{4},e})$ |
17.直线x+2y-5+$\sqrt{5}$=0被圆x2+y2-2x-4y=0截得的弦长( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | 4 | D. | 4$\sqrt{6}$ |
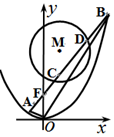 已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.