题目内容
16．在△ABC中，a=2，cos C=-$\frac{1}{4}$，3sin A=2sin B，则c=4．分析 由题意和正弦定理化简后求出b的值，由余弦定理求出c的值．
解答 解：由题意知，3sin A=2sin B，
由正弦定理得，3a=2b，
又a=2，则b=3，且cosC=$-\frac{1}{4}$，
由余弦定理得，c2=a2+b2-2abcosC
=4+9-2×2×3×（$-\frac{1}{4}$）=16，
所以c=4，
故答案为：4．
点评 本题考查了正弦定理和余弦定理的应用，属于基础题．
练习册系列答案
相关题目
1．直线y=mx+1与曲线x=2+$\sqrt{1-{y}^{2}}$的图象始终有交点，则m的取值范围是（ ）
| A． | （-1，0） | B． | [-1，0] | C． | （-1，-$\frac{1}{3}$） | D． | [-1，-$\frac{1}{3}$] |
8．若命题“p且q”为假，且p为真，则（ ）
| A． | “p或q”为假 | B． | q为假 | C． | q为真 | D． | 不能判断q的真假 |
5．已知N是自然数集，在数轴上表示出集合A，如果所示，则A∩N=（ ）
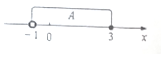
| A． | {-1，0，1，2，3} | B． | {0，1，2，3} | C． | {1，2，3} | D． | {2，3} |
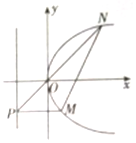双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1（a＞0）$的左、右焦点分别为F1，F2，过F2作x轴垂直的直线交双曲线C于A、B两点，△F1AB的面积为12，抛物线E：y2=2px（p＞0）以双曲线C的右顶点为焦点．