题目内容
已知定义在R上的函数f（x）满足f（x+1）=-f（x），当x∈[-1，1]时，f（x）=x2，函数g（x）=
，若函数h（x）=f（x）-g（x）在区间[-5，5]上恰有8个零点，则a的取值范围为
（ ）
|
（ ）
| A、（2，4） |
| B、（2，5） |
| C、（1，5） |
| D、（1，4） |
考点：函数零点的判定定理
专题：计算题,作图题,函数的性质及应用
分析：函数h（x）=f（x）-g（x）在区间[-5，5]上恰有8个零点即函数f（x）与函数g（x）在区间[-5，5]上有8个交点，从而作图求解．
解答：
解：函数h（x）=f（x）-g（x）在区间[-5，5]上恰有8个零点即
函数f（x）与函数g（x）在区间[-5，5]上有8个交点，
由f（x+1）=-f（x）=f（x-1）知，
f（x）是R上周期为2的函数，
作函数f（x）与函数g（x）在区间[-5，5]上的图象如下，
由图象知，当x∈[-5，1]时，图象有5个交点，故在[1，5]上有3个交点即可；
故
；
解得，2＜a＜4；
故选A．
函数f（x）与函数g（x）在区间[-5，5]上有8个交点，
由f（x+1）=-f（x）=f（x-1）知，
f（x）是R上周期为2的函数，
作函数f（x）与函数g（x）在区间[-5，5]上的图象如下，
由图象知，当x∈[-5，1]时，图象有5个交点，故在[1，5]上有3个交点即可；
故
|
解得，2＜a＜4；
故选A．
点评：本题考查了函数的零点与图象的关系应用，属于基础题．
练习册系列答案
相关题目
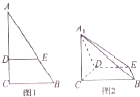如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E分别是AC，AB上的点，且DE∥BC，DE=2，将△ADE沿DE折起到A1DE的位置，使A2C⊥CD，如图2．
如图是一个正方体的平面展开图，则在正方体中，①CN与BE是异面直线；②平面DEM∥平面ACF；③DE⊥BM； ④AF与BM所成角为60°；⑤BN⊥平面AFC，在以上的五个结论中，正确的是
某校举行演讲比赛，9位评委给选手A打出的分数如茎叶图所示，统计员在去掉一个最高分和一个最低分后，算得平均分为91，复核员在复核时，发现有一个数字（茎叶图中的x）无法看清，若统计员计算无误，则数字x应该是（ ）