题目内容
已知函数f(x)=|x﹣4|﹣t,t∈R,且关于x的不等式f(x+2)≤2的解集为[﹣1,5].
(1)求t值;
(2)a,b,c均为正实数,且a+b+c=t,求证: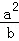 +
+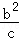 +
+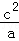 ≥1.
≥1.
(1) ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)首先解不等式 ,根据题设列方程解出
,根据题设列方程解出 的值.
的值.
(2)要证 ,只要证:
,只要证: ,即证
,即证
试题解析:【解析】
(1)由f(x+2)≤2得|x﹣4|﹣t≤2,
∴当t+2≥0时,解得﹣t≤x≤t+4,
又∵不等式f(x+2)≤2的解集为[﹣1,5],
∴﹣t=﹣1且t+4=5,∴t=1.
(2)∵a,b,c均为正实数,且a+b+c=1,
∴ +
+ +
+ +(a+b+c)=(
+(a+b+c)=( )+(
)+( +c)+(
+c)+( +a)≥2
+a)≥2 +2
+2 +2
+2 =2(a+b+c)=2
=2(a+b+c)=2
∴ +
+ +
+ ≥1.
≥1.
考点:1、含绝对值的不等式的解法;2、基本不等式.

 计算高手系列答案
计算高手系列答案(12分)某市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由于空气污染造成的经济损失为S(单位:元),空气质量指数API为ω,在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当API为150时造成的经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的经济损失为2000元.
(1)试写出S(ω)表达式;
(2)试估计在本年内随机抽取一天,该天经济损失S大于500元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
P(K2≥kc) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
Kc | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
 ,其中
,其中 .
. 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为 ,求a的值.
,求a的值.
 (
( ),则双曲线
),则双曲线 的离心率等于( )
的离心率等于( ) B.
B. C.
C. D.
D.
 到实数集
到实数集 的映射过程:区间
的映射过程:区间 中的实数
中的实数 对应数轴上的点
对应数轴上的点 (点
(点 对应实数
对应实数 ,点
,点 对应实数
对应实数 ),如图①;将线段
),如图①;将线段 围成一个圆,使两端点
围成一个圆,使两端点 、
、 恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点
轴上,点 的坐标为
的坐标为 ,在图形变化过程中,图①中线段
,在图形变化过程中,图①中线段 的长度对应于图③中的弧
的长度对应于图③中的弧 的长度,如图③,图③中直线
的长度,如图③,图③中直线 与
与 轴交于点
轴交于点 ,则
,则 的象就是
的象就是 ,记作
,记作 .给出下列命题:①
.给出下列命题:① ;②
;② ;③
;③ 是奇函数;④
是奇函数;④ 在定义域上单调递增,则所有真命题的序号是( )
在定义域上单调递增,则所有真命题的序号是( )

 (
( ),直线
),直线 过
过 的一个焦点,且垂直于
的一个焦点,且垂直于 轴,直线
轴,直线 与双曲线
与双曲线 交于
交于 ,
, 两点,则
两点,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 <x1x2<1 B.1<x1x2<e
<x1x2<1 B.1<x1x2<e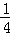 ,乙每次投中的概率为
,乙每次投中的概率为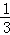 求:
求: 的首项
的首项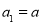 ,其前
,其前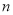 和为
和为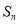 ,且满足
,且满足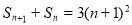 (
(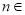 N*).
N*).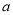 表示
表示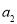 的值;
的值;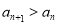 ,求实数
,求实数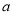 的取值范围.
的取值范围.