题目内容
设函数 ,其中
,其中 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若不等式 的解集为
的解集为 ,求a的值.
,求a的值.
(1) 或
或 .(2)
.(2)
【解析】
试题分析:(1) 时
时




 或
或 ;
;
(2)去掉绝对值符号,得不等式的解集为 ,由
,由 =
=  得故
得故 。
。
试题解析:(1)当 时,
时, 可化为
可化为 .
.
由此可得  或
或 .
.
故不等式 的解集为
的解集为 或
或 .
.
(2)由 得
得
 此不等式化为不等式组
此不等式化为不等式组
 或
或 , 即
, 即  或
或
因为 ,所以不等式组的解集为
,所以不等式组的解集为 ,由题设可得
,由题设可得 =
=  ,故
,故
考点:函数与不等式、含绝对值不等式的解法.

练习册系列答案
相关题目
 +z
+z =0”是“z1=z2=0”的 ( )
=0”是“z1=z2=0”的 ( ) 展开式的常数项为 .
展开式的常数项为 . (用数字作答)
(用数字作答) 和函数
和函数 ,若
,若 的反函数为
的反函数为 ,则
,则 与
与 两图象交点的个数为( )
两图象交点的个数为( ) B.
B. C.
C. D.
D.
 ,做对两道题的概率为
,做对两道题的概率为 ,则预估计做对第二道题的概率为( )
,则预估计做对第二道题的概率为( ) B.
B.
 D.
D.
 的前
的前 项和
项和 .
. 是等比数列,公比为
是等比数列,公比为 且
且
 ,求数列
,求数列 .
. :函数
:函数 的图象恒过定点
的图象恒过定点 ;命题
;命题 :若函数
:若函数
 为偶函数,则函数
为偶函数,则函数
 的图象关于直线
的图象关于直线 对称,则下列命题为真命题的是( )
对称,则下列命题为真命题的是( )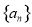 是等差数列,
是等差数列, ,
, .
. 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前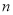 项和
项和 .
.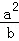 +
+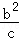 +
+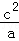 ≥1.
≥1.