题目内容
(本小题满分14分)已知数列 的首项
的首项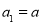 ,其前
,其前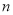 和为
和为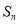 ,且满足
,且满足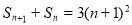 (
(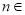 N*).
N*).
(1)用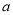 表示
表示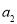 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)对任意的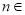 N*,
N*,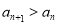 ,求实数
,求实数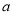 的取值范围.
的取值范围.
(1)12-2a;(2)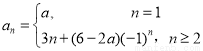 ;(3).
;(3).
【解析】
试题分析:根据递推关系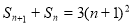 ,即可用
,即可用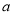 表示
表示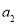 的值;(2)由条件
的值;(2)由条件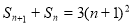 得,
得,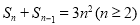 ,两式相减得
,两式相减得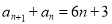
 ,解法1:故
,解法1:故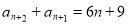 ,
,
两式再相减得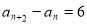
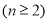 ,
,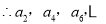 构成以
构成以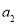 为首项,公差为6的等差数列;
为首项,公差为6的等差数列; 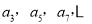 构成以
构成以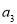 为首项,公差为6的等差数列;由(1)得
为首项,公差为6的等差数列;由(1)得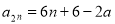 ;由条件
;由条件 得
得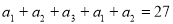 ,得
,得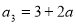 ,从而
,从而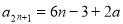 , 即可求出结果;解法2:设
, 即可求出结果;解法2:设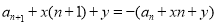 ,即
,即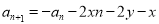 则
则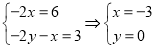 ,则有
,则有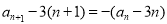 ,当
,当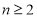 时,
时,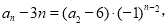 即
即 即可求出结果;(3)对任意的
即可求出结果;(3)对任意的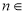 N*,
N*,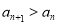 , 当
, 当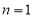 时,由
时,由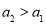 ,有
,有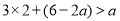 得
得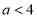 ①;
①;
当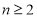 时,由
时,由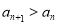 ,有
,有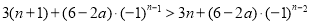 ,即
,即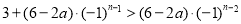 ,对n进行分类讨论解不等式,即可求出结果.
,对n进行分类讨论解不等式,即可求出结果.
试题解析:解析:(1)由条件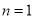 得
得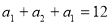 ,
, 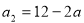 . 2分
. 2分
(2)由条件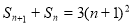 得,
得,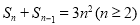 3分
3分
两式相减得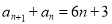
 ,
,
解法1:
故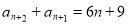 ,
,
两式再相减得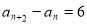
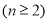 ,
,
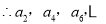 构成以
构成以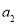 为首项,公差为6的等差数列;
为首项,公差为6的等差数列;
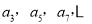 构成以
构成以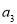 为首项,公差为6的等差数列; 5分
为首项,公差为6的等差数列; 5分
由(1)得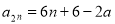 ;
;
由条件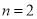 得
得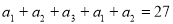 ,得
,得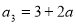 ,
,
从而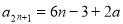 ,
,

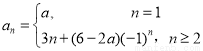 9分
9分
解法2:
设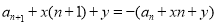 ,即
,即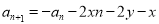
则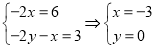
 有
有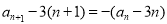

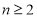 时,
时,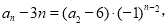 即
即

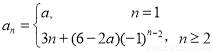 9分
9分
(3)对任意的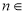 N*,
N*,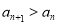 ,
,
当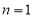 时,由
时,由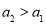 ,有
,有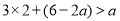 得
得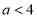 ①;
①;
当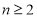 时,由
时,由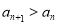 ,有
,有
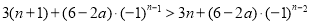 ,即
,即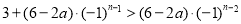
若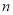 为偶数,则
为偶数,则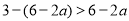 得
得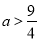 ②;
②;
若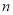 为奇数,则
为奇数,则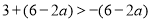 得
得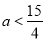 ③.
③.
由①、②、③得 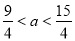 . 14分.
. 14分.
考点:1.数列的递推公式;2.恒成立问题.

练习册系列答案
相关题目
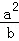 +
+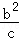 +
+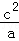 ≥1.
≥1.
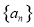 的公差
的公差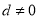 ,且
,且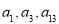 成等比数列,若
成等比数列,若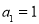 ,
, 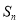 为数列
为数列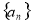 的前
的前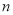 项和,则
项和,则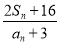 的最小值为 ( )
的最小值为 ( )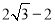 D.
D.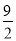
 且,
且, 与
与 共线,那么
共线,那么 的值为 ( )
的值为 ( )  ,且
,且 依次成等比数列,设
依次成等比数列,设 ,则
,则 这三个数的大小关系为 .
这三个数的大小关系为 . 终边上一点
终边上一点 的坐标是
的坐标是 ,则
,则
 B.
B. C.
C. D.
D.
 由满足:对任意
由满足:对任意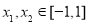 时,都有
时,都有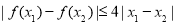 的函数
的函数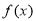 组成.对于两个函数
组成.对于两个函数 ,以下关系成立的是
,以下关系成立的是 B.
B.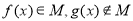
 D.
D.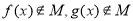
 (
( ,
, )的部分图象如图所示,则
)的部分图象如图所示,则 的值为 .
的值为 .