��Ŀ����
��ͼչʾ��һ�������� ��ʵ����
��ʵ���� ��ӳ����̣�����
��ӳ����̣����� �е�ʵ��
�е�ʵ�� ��Ӧ�����ϵĵ�
��Ӧ�����ϵĵ� ����
���� ��Ӧʵ��
��Ӧʵ�� ����
���� ��Ӧʵ��
��Ӧʵ�� ������ͼ�٣����߶�
������ͼ�٣����߶� Χ��һ��Բ��ʹ���˵�
Χ��һ��Բ��ʹ���˵� ��
�� ǡ���غϣ���ͼ�ڣ��ٽ����Բ����ƽ��ֱ������ϵ�У�ʹ��Բ����
ǡ���غϣ���ͼ�ڣ��ٽ����Բ����ƽ��ֱ������ϵ�У�ʹ��Բ���� ���ϣ���
���ϣ��� ������Ϊ
������Ϊ ����ͼ�α仯�����У�ͼ�����߶�
����ͼ�α仯�����У�ͼ�����߶� �ij��ȶ�Ӧ��ͼ���еĻ�
�ij��ȶ�Ӧ��ͼ���еĻ� �ij��ȣ���ͼ�ۣ�ͼ����ֱ��
�ij��ȣ���ͼ�ۣ�ͼ����ֱ�� ��
�� �ύ�ڵ�
�ύ�ڵ� ����
���� �������
������� ������
������ �������������⣺��
�������������⣺�� ����
���� ����
���� ���溯������
���溯������ �ڶ������ϵ��������������������������ǣ� ��
�ڶ������ϵ��������������������������ǣ� ��

A���٢� B���ڢ� C���٢� D���ڢ�
D
��������
������������� ������
������ ʱ��
ʱ�� ��ĺ�������һ��������������1���ʢٴ��ģ���
��ĺ�������һ��������������1���ʢٴ��ģ��� ʱ����
ʱ���� ������ԭ�㣬��
������ԭ�㣬�� ������
������ ���ʢ���ȷ��
���ʢ���ȷ�� ���Ա�����������
���Ա����������� ��ֵ���ʶ�����Ϊ��0��1��������ֵ��ΪN��ĺ����궨������ԭ��Գƣ����Ժ���
��ֵ���ʶ�����Ϊ��0��1��������ֵ��ΪN��ĺ����궨������ԭ��Գƣ����Ժ��� �����溯�����ʢ��Ǵ��ģ�����mֵ��0����1��N���ڲ��������ƶ����ʺ���ֵ�Dz�������ģ���Ϊ����������ȷ.����ӦѡD.
�����溯�����ʢ��Ǵ��ģ�����mֵ��0����1��N���ڲ��������ƶ����ʺ���ֵ�Dz�������ģ���Ϊ����������ȷ.����ӦѡD.
���㣺�¶������⣬ӳ�䡢�������弰���������ԡ���ż��.

��ϰ��ϵ�д�
�����Ŀ
 �ͺ���
�ͺ��� ����
���� �ķ�����Ϊ
�ķ�����Ϊ ����
���� ��
�� ��ͼ��ĸ���Ϊ�� ��
��ͼ��ĸ���Ϊ�� �� B��
B�� C��
C�� D��
D��
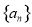 �ǵȲ����У�
�ǵȲ����У� ��
�� ��
�� ��ͨ�ʽ��
��ͨ�ʽ�� ��������
�������� ��ǰ
��ǰ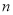 ���
��� ��
�� ��
�� ��
�� ��һ��ʵ��
��һ��ʵ�� ����������
���������� ��ȡֵ��Χ��
��ȡֵ��Χ�� �ǹ��Ϊ
�ǹ��Ϊ �ĵȲ����У�
�ĵȲ����У� ����
���� ��
�� ��
�� �ɵȱ����У�
�ɵȱ����У� ��ͨ�ʽ��
��ͨ�ʽ�� ��������
�������� ��ǰ
��ǰ ���
��� ��
�� ��
�� ��
�� ������
������ ����
���� �� ��
�� �� B��
B�� C��
C�� D��
D��
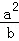 +
+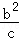 +
+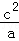 ��1��
��1��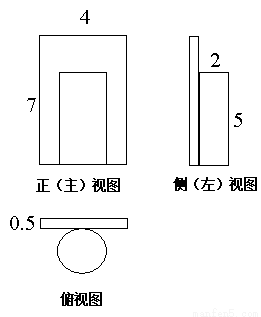
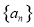 ����
����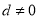 ����
����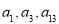 �ɵȱ����У���
�ɵȱ����У���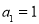 ��
�� 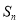 ����
Ϊ����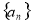 ��ǰ
��ǰ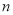 ��ͣ���
��ͣ���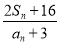 ����СֵΪ �� ��
����СֵΪ �� ��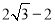 D��
D��