题目内容
(12分)甲、乙两人玩投篮游戏,规则如下:两人轮流投篮,每人至多投2次,甲先投,若有人投中即停止投篮,结束游戏,已知甲每次投中的概率为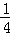 ,乙每次投中的概率为
,乙每次投中的概率为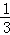 求:
求:
(Ⅰ)乙投篮次数不超过1次的概率.
(Ⅱ)记甲、乙两人投篮次数和为ξ,求ξ的分布列和数学期望.
(Ⅰ)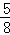 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(I)记“甲投篮投中”为事件A,“乙投篮投中”为事件B,由题设条件,“乙投篮次数不超过1次”包括三种情况:一种是甲第1次投篮投中,另一种是甲第1次投篮未投中而乙第1次投篮投中,再一种是甲、乙第1次投篮均未投中而甲第2次投篮投中,利用互斥事件的概率公式即可求解;
(II)由题意知甲、乙投篮总次数ξ的取值1,2,3,4,分别求出相应的概率,即可得到ξ的分布列与期望.
试题解析:【解析】
(I)记“甲投篮投中”为事件A,“乙投篮投中”为事件 B.
“乙投篮次数不超过1次”包括三种情况:一种是甲第1次投篮投中,另一种是甲第1次投篮未投中而乙第1次投篮投中,再一种是甲、乙第1次投篮均未投中而甲第2次投篮投中,
所求的概率是P=P(A+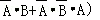
=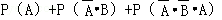 =
=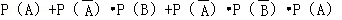
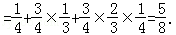
乙投篮次数不超过1次的概率为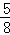 (7分)
(7分)
(2)甲、乙投篮总次数ξ的取值1,2,3,4,
P(ξ=1)=P(A)= ;
;
P(ξ=2)=P(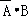 )=
)=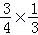 =
= ;
;
P(ξ=3)=P(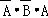 )=
)=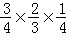 =
= ;
;
P(ξ=4)=P(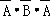 )=
)=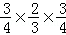 =
=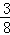 ;
;
甲、乙投篮次数总和ξ的分布列为:
ξ 1 2 3 4
P 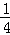
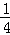
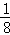
 (11分)
(11分)
甲、乙投篮总次数ξ的数学期望为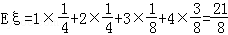 (13分)
(13分)
考点:1、互斥事件与对立事件;2、离散型随机变量的期望与方差.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
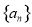 是等差数列,
是等差数列, ,
, .
. 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前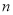 项和
项和 .
.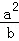 +
+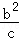 +
+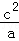 ≥1.
≥1.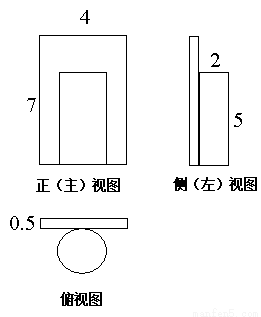
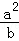 +
+ +
+ ≥1.
≥1.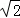 ,cosC=﹣
,cosC=﹣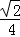 ,则sinB= _________ .
,则sinB= _________ .
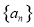 的公差
的公差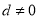 ,且
,且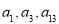 成等比数列,若
成等比数列,若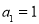 ,
, 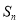 为数列
为数列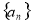 的前
的前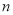 项和,则
项和,则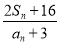 的最小值为 ( )
的最小值为 ( )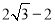 D.
D.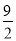
 由满足:对任意
由满足:对任意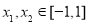 时,都有
时,都有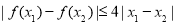 的函数
的函数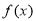 组成.对于两个函数
组成.对于两个函数 ,以下关系成立的是
,以下关系成立的是 B.
B.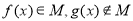
 D.
D.