题目内容
16.已知等差数列{an}的前5项的和为55,且a6+a7=36.(1)求数列{an}的通项公式;
(2)设数列bn=$\frac{1}{({a}_{n}-6)({a}_{n}-4)}$,求数列{bn}的前n项和Sn.
分析 (1)由等差数列通项公式和前n项和公式列出方程组,求出首项与公差,由此能求出数列{an}的通项公式.
(2)由bn=$\frac{1}{({a}_{n}-6)({a}_{n}-4)}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,利用裂项求和法能求出数列{bn}的前n项和.
解答 解:(1)∵等差数列{an}的前5项的和为55,且a6+a7=36,
∴$\left\{\begin{array}{l}{5{a}_{1}+\frac{5×4}{2}d=55}\\{{a}_{1}+5d+{a}_{1}+6d=36}\end{array}\right.$,
解得a1=7,d=2,
∴数列{an}的通项公式an=7+(n-1)×2=2n+5.
(2)bn=$\frac{1}{({a}_{n}-6)({a}_{n}-4)}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴数列{bn}的前n项和:
Sn=$\frac{1}{2}(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$
=$\frac{1}{2}(1-\frac{1}{2n+1})$
=$\frac{n}{2n+1}$.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
4.已知函数f(x)=ax3-6x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( )
| A. | (-∞,-4) | B. | (4,+∞) | C. | (-∞,-4$\sqrt{2}$) | D. | (4$\sqrt{2}$,+∞) |
1.若反比例函数f(x)=$\frac{k}{x}$的图象在第一象限内单调递减,则k的取值范围( )
| A. | k≥0 | B. | k≤0 | C. | k>0 | D. | k<0 |
5.一个几何体的顶点都在球面上,这个几何体的三视图如图所示,该球的表面积是( )
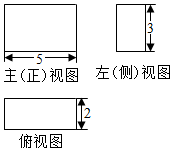

| A. | 19π | B. | 30π | C. | 38π | D. | $\frac{{19\sqrt{38}}}{3}π$ |