题目内容
17. 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,AB⊥BC,PA=6,AB=BC=8,DF=5.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,AB⊥BC,PA=6,AB=BC=8,DF=5.(1)求证:直线PA∥平面DEF;
(2)求证:平面BDE⊥平面ABC;
(3)求直线PB与平面PAC所成角的正弦值.
分析 (1)由D、E为PC、AC的中点,得出DE∥PA,从而得出PA∥平面DEF;
(2)要证平面BDE⊥平面ABC,只需证DE⊥平面ABC,即证DE⊥EF,且DE⊥AC即可;
(3)证明BE⊥平面PAC.连接PE,则∠BPE即为所求.
解答 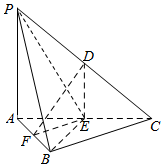 (1)证明:由于D,E分别是PC,AC的中点,则有PA∥DE,
(1)证明:由于D,E分别是PC,AC的中点,则有PA∥DE,
又PA?平面DEF,DE?平面DEF,所以PA∥平面DEF …(4分)
(2)证明:由(1)知PA∥DE,又PA⊥AC,所以DE⊥AC,
又F是AB的中点,$所以DE=\frac{1}{2}PA=3,EF=\frac{1}{2}BC=4,又DF=5,所以D{E^2}+E{F^2}=D{F^2}$,
所以DE⊥EF,
又EF∩AC=E,所以DE⊥平面ABC,
又DE?平面BDE,所以平面BDE⊥平面ABC.(8分)
(3)解:由(2)知DE⊥平面ABC,又DE?平面PAC,所以平面PAC⊥平面ABC,
又平面PAC∩平面ABC=AC,BE⊥AC,BE?平面ABC,所以BE⊥平面PAC.
连接PE,则∠BPE即为所求.
$BE=4\sqrt{2},PB=10$,故$sin∠BPE=\frac{{2\sqrt{2}}}{5}$.…(12分)
点评 本题考查了空间中的平行与垂直问题,考查线面角,解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系,是中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
8.已知全集A={x∈N|x<2},B={0,1,2},则A∩B=( )
| A. | {1,2} | B. | {0,1,2} | C. | {1} | D. | {0,1} |