题目内容
15.命题“?x∈[1,2],x2-a≤0”为真命题的一个充要条件是( )| A. | a≥4 | B. | a≤4 | C. | a≥5 | D. | a≤5 |
分析 根据不等式恒成立,利用参数分离法转化为求函数的最值即可得到结论.
解答 解:若“?x∈[1,2],x2-a≤0,
则a≥x2,x∈[1,2],
∵y=x2,x∈[1,2],
∴1≤y≤4,
即a≥4,
即命题“?x∈[1,2],x2-a≤0”为真命题的一个充要条件是a≥4,
故选:A
点评 本题主要考查充分条件和必要条件的判断,根据不等式恒成立,求出函数的最值是解决本题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.对整数n≥3,记f(n)=log23•log34…logn-1n,则f(22)+f(23)+…+f(210)=( )
| A. | 55 | B. | 1024 | C. | 54 | D. | 1000 |
20.已知集合M={(x,y)|x+y-2≤0,x≥0,y≥0},集合N={$(x,y)|y≤\sqrt{x},y≥0$},若点P∈M,则P∈M∩N的概率为( )
| A. | $\frac{7}{18}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{3}{4}$ |
4.已知函数f(x)=ax3-6x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( )
| A. | (-∞,-4) | B. | (4,+∞) | C. | (-∞,-4$\sqrt{2}$) | D. | (4$\sqrt{2}$,+∞) |
5.一个几何体的顶点都在球面上,这个几何体的三视图如图所示,该球的表面积是( )
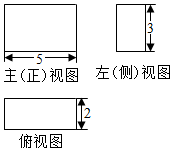

| A. | 19π | B. | 30π | C. | 38π | D. | $\frac{{19\sqrt{38}}}{3}π$ |