题目内容
10.已知a>0且a≠1,设命题p:函数y=loga(x+1)在区间(-1,+∞)内单调递减;q:曲线y=x2+(2a-3)x+1与x轴有两个不同的交点.如果p或q为真命题,那么a的取值集合是怎样的呢?并写出求解过程.分析 分别求出p,q成立的a的范围,根据复合命题的真假,求出a的范围即可.
解答 解:先看命题p:
∵函数y=loga(x+1)在(-1,+∞)内单调递减,a>0,a≠1,
∴命题p为真时?0<a<1;
再看命题q:
当命题q为真时,二次函数对应的一元二次方程根的判别式满足
△=(2a-3)2-4>0⇒0<a<$\frac{1}{2}$或a>$\frac{5}{2}$;
如果p或q为真命题,则p真或q真,
故0<a<1或a>$\frac{5}{2}$.
点评 本题以函数的单调性和二次函数零点的问题为载体,考查了命题真假的判断与应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知条件p:函数$y=\sqrt{\frac{x-1}{x+3}}$的定义域,条件q:5x-6>x2,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
19.过双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的右焦点F作双曲线的一条渐近线的垂线,垂足为E,O为坐标原点,若∠OFE=2∠EOF,则b=( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{3}$ |
20.某几何体的三视图如图所示,则该几何体的表面积为( )
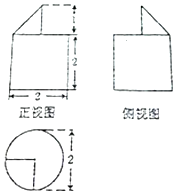

| A. | 6π+1 | B. | $\frac{{({24+\sqrt{2}})π}}{4}+1$ | C. | $\frac{{({23+\sqrt{2}})π}}{4}+\frac{1}{2}$ | D. | $\frac{{({23+\sqrt{2}})π}}{4}+1$ |
 如图,在△ABC中,∠BAC=90°,AB=6,D在斜边BC上,且CD=3DB,则$\overrightarrow{AB}•\overrightarrow{CD}$=27.
如图,在△ABC中,∠BAC=90°,AB=6,D在斜边BC上,且CD=3DB,则$\overrightarrow{AB}•\overrightarrow{CD}$=27. 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.