题目内容
10．已知实数x、y满足$\left\{\begin{array}{l}2x-y≤0\\ x-3y+5≥0\\ x＞0\\ y＞0\end{array}\right.$，则z=2x+y的最大值为4．分析 作出约束条件对应的区域，由目标函数的特征由线性规划规律求出z=2x+y的最大值．
解答 
解：不等式组$\left\{\begin{array}{l}2x-y≤0\\ x-3y+5≥0\\ x＞0\\ y＞0\end{array}\right.$，对应的可行域如图：
目标函数是z=2x+y，由$\left\{\begin{array}{l}{2x-y=0}\\{x-3y+5=0}\end{array}\right.$解得A（1，2）
当目标函数对应直线过点A（1，2）时，z取到最大值为4．
故答案为：4．
点评 本题考查线性规划，是线性规划中求最值的常规题型．其步骤是作图，找点，求值．
练习册系列答案
名师点拨卷系列答案
相关题目
19．设f，g都是由A到A的映射，其对应法则如表所示（从上到下），则与f[g（1）]相同的是（ ）
表1 映射f的对应法则
表2 映射g的对应法则
表1 映射f的对应法则
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 3 | 4 | 2 | 1 |
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 4 | 3 | 1 | 2 |
| A． | g[f（3）] | B． | g[f（1）] | C． | f[f（4）] | D． | f[f（3）] |
20．
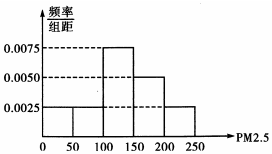PM2.5是衡量空气污染程度的一个指标，为了了解某市空气质量情况，从去年每天的PM2.5值的数据中随机抽取40天的数据，其频率分布直方图如图所示．现将PM2.5的值划分为如下等级
（1）根据样本空气质量PM2.5的数据的频率分布直方图完成下列分布表；
（2）估计该市在下一年的360天中空气质量为一级天气的天数；
（3）在样本中，按照分层抽样的方法从一级天气，三级天气，四级天气的PM2.5值的数据中抽取5天的数据，再从这5个数据中随机抽取2个，求至少一天是一级天气的概率．
PM2.5是衡量空气污染程度的一个指标，为了了解某市空气质量情况，从去年每天的PM2.5值的数据中随机抽取40天的数据，其频率分布直方图如图所示．现将PM2.5的值划分为如下等级| PM2.5 | [0，100） | [100，150） | [150，200） | [200，250] |
| 等级 | 一级 | 二级 | 三级 | 四级 |
| PM2.5 | [0，50） | [50，100） | [100，150） | [150，200） | [200，250] |
| 天数 | 5 | 5 | 15 | 10 | 5 |
（3）在样本中，按照分层抽样的方法从一级天气，三级天气，四级天气的PM2.5值的数据中抽取5天的数据，再从这5个数据中随机抽取2个，求至少一天是一级天气的概率．