题目内容
15.已知$p:-2≤1-\frac{x-1}{3}≤2,q:({x+m-1})({x-m-1})≤0({m>0})$,且q是p的必要不充分条件,求实数m的取值范围.分析 解出关于p,q的不等式,根据充分必要条件的定义顶顶顶关于m的不等式组,解出即可.
解答 解:∵$p:-2≤1-\frac{x-1}{3}≤2,q:({x+m-1})({x-m-1})≤0({m>0})$,
∴p:-2≤x≤10,q:1-m≤x≤1+m,(m>0),
∵q是p的必要不充分条件,
∴$\left\{{\begin{array}{l}{1-m≤-2}\\{1+m≥10}\end{array}}\right.$,
∴m≥9.
点评 本题考查了充分必要条件,考查不等式的解法,是一道基础题.

练习册系列答案
相关题目
20.设变量x,y满足约束条件$\left\{\begin{array}{l}x+y≥2\\ 2x+y≥2\\ x-y≤2\end{array}\right.$目标函数z=x-2y的最大值是( )
| A. | -4 | B. | 2 | C. | $\frac{8}{3}$ | D. | $\frac{16}{3}$ |
7.将y=cosx的图象上的所有点的纵坐标不变,横坐标缩小到原来的一半,然后再将图象沿x轴负方向平移$\frac{π}{4}$个单位,则所得图象的解析式为( )
| A. | y=sinx | B. | y=-sin2x | C. | $y=cos({2x+\frac{π}{4}})$ | D. | $y=cos({\frac{x}{2}+\frac{π}{4}})$ |
4.已知双曲线mx2+y2=1(m∈R)与椭圆${x^2}+\frac{y^2}{5}=1$有相同的焦点,则该双曲线的渐近线方程为( )
| A. | $y=±\sqrt{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{3}x$ | C. | $y=±\frac{1}{3}x$ | D. | y=±3x |
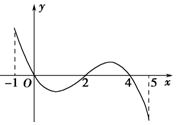 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题: