题目内容
下列命题正确的是（ ）
| A、若两条直线和同一个平面所成的角相等，则这两条直线平行 |
| B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 |
| C、若两个平面都垂直于第三个平面，则这两个平面平行 |
| D、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 |
考点：空间中直线与平面之间的位置关系,空间中直线与直线之间的位置关系
专题：综合题,空间位置关系与距离
分析：A，B，C列举所有情况，D考虑线面平行的性质定理及平行公理即可．
解答：
解：对于A，两条直线和同一个平面所成的角相等，则这两条直线平行、相交、异面都有可能，故不正确；
对于B，一个平面内有三个点到另一个平面的距离相等，则这两个平面平行或相交，故不正确；
对于C，两个平面都垂直于第三个平面，则这两个平面平行或相交，故不正确；
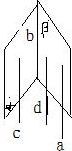
对于D，由a∥α得，经过a的平面与α相交于直线c，则a∥c，同理，设经过a的平面与β相交于直线d，则a∥d，由平行公理得：c∥d，则c∥β，又c?α，α∩β=b，所以c∥b，又a∥c，所以a∥b．
故选：D．
解：对于A，两条直线和同一个平面所成的角相等，则这两条直线平行、相交、异面都有可能，故不正确；对于B，一个平面内有三个点到另一个平面的距离相等，则这两个平面平行或相交，故不正确；
对于C，两个平面都垂直于第三个平面，则这两个平面平行或相交，故不正确；
对于D，由a∥α得，经过a的平面与α相交于直线c，则a∥c，同理，设经过a的平面与β相交于直线d，则a∥d，由平行公理得：c∥d，则c∥β，又c?α，α∩β=b，所以c∥b，又a∥c，所以a∥b．
故选：D．
点评：本题主要考查了空间线面位置关系，要求熟练掌握相应的定义和定理，注意定理成立的条件．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
（理）若a=
（x-1）dx，b=
（ex-1）dx，c=
（sinx-1）dx，则（ ）
| ∫ | 1 0 |
| ∫ | 1 0 |
| ∫ | 1 0 |
| A、a＜b＜c |
| B、b＜c＜a |
| C、c＜a＜b |
| D、a＜c＜b |
定义在R上的函数f（x）=e|x|+ln
，且f（x+t）＞f（x）在x∈（-1，+∞）上恒成立，则关于x的方程f（2x-1）=f（t）-e的根的个数叙述正确的是（ ）
| x2+1 |
| A、有两个 | B、有一个 |
| C、没有 | D、上述情况都有可能 |
若直线m不平行于平面α，且m?α，则下列结论成立的是（ ）
| A、α内的所有直线与m异面 |
| B、α内的直线与m都相交 |
| C、α内存在唯一的直线与m平行 |
| D、α内不存在与m平行的直线 |
设z=x+y，其中x，y满足
，当z的最大值为6时，k的值为（ ）
|
| A、3 | B、4 | C、5 | D、6 |