题目内容
设a,b>0,a≠b,lna-lnb=a-b,给出下列结论,
①0<ab<1,②O<a+b<2,③a+b-ab>1.
其中所有正确结论的序号是 .
①0<ab<1,②O<a+b<2,③a+b-ab>1.
其中所有正确结论的序号是
考点:对数的运算性质
专题:函数的性质及应用,导数的综合应用
分析:由lna-lnb=a-b,化为lna-a=lnb-b.令f(x)=lnx-x,(x>0),利用导数可得函数f(x)的单调性,画出图象.不妨设0<a<b.0<a<1<b.0<
<1.
①证明ab<1,只要证明a<
,即可,即证明lnb-b<ln
-
,构造函数g(b),利用导数研究其单调性即可得出.
②由图象可得b-1>1-a,可得a+b>2,即可判断出正误;
③由图象可得:(a-1)(b-1)<0,化简即可判断出正误.
| 1 |
| b |
①证明ab<1,只要证明a<
| 1 |
| b |
| 1 |
| b |
| 1 |
| b |
②由图象可得b-1>1-a,可得a+b>2,即可判断出正误;
③由图象可得:(a-1)(b-1)<0,化简即可判断出正误.
解答:
解:lna-lnb=a-b,化为lna-a=lnb-b.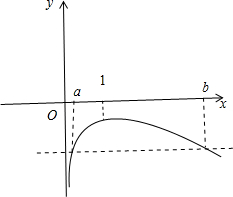
令f(x)=lnx-x,(x>0),
f′(x)=
-1=
,
当x>1时,f′(x)<0,此时函数f(x)单调递减;当0<x<1时,f′(x)>0,此时函数f(x)单调递增.
∴当x=1时,函数f(x)取得最大值,f(1)=-1.
∵a,b>0,a≠b,不妨设0<a<b.
又f(a)=f(b),
则0<a<1<b,0<
<1.
①证明ab<1,只要证明a<
,
∵0<a<
<1,
∴只要证明f(a)<f(
)即可,
∵f(a)=f(b),
∴只要证明f(b)<f(
)即可,
即证明lnb-b<ln
-
,
化为g(b)=2lnb-b+
<0,(b>1).
g′(b)=
-1-
=
<0,
∴函数g(b)在b>1时单调递减,
∴g(b)<g(1)=0,
因此f(b)<f(
)成立,即f(a)<f(
)成立,
∴a<
<1,
∴0<ab<1正确,①正确.
②由图象可得b-1>1-a,∴a+b>2,∴②不正确;
③∵(a-1)(b-1)<0,∴a+b-ab>1,因此③正确.
综上可得:①③正确.
故答案为:①③.

令f(x)=lnx-x,(x>0),
f′(x)=
| 1 |
| x |
| 1-x |
| x |
当x>1时,f′(x)<0,此时函数f(x)单调递减;当0<x<1时,f′(x)>0,此时函数f(x)单调递增.
∴当x=1时,函数f(x)取得最大值,f(1)=-1.
∵a,b>0,a≠b,不妨设0<a<b.
又f(a)=f(b),
则0<a<1<b,0<
| 1 |
| b |
①证明ab<1,只要证明a<
| 1 |
| b |
∵0<a<
| 1 |
| b |
∴只要证明f(a)<f(
| 1 |
| b |
∵f(a)=f(b),
∴只要证明f(b)<f(
| 1 |
| b |
即证明lnb-b<ln
| 1 |
| b |
| 1 |
| b |
化为g(b)=2lnb-b+
| 1 |
| b |
g′(b)=
| 2 |
| b |
| 1 |
| b2 |
| -(b-1)2 |
| b2 |
∴函数g(b)在b>1时单调递减,
∴g(b)<g(1)=0,
因此f(b)<f(
| 1 |
| b |
| 1 |
| b |
∴a<
| 1 |
| b |
∴0<ab<1正确,①正确.
②由图象可得b-1>1-a,∴a+b>2,∴②不正确;
③∵(a-1)(b-1)<0,∴a+b-ab>1,因此③正确.
综上可得:①③正确.
故答案为:①③.
点评:本题考查了利用导数研究函数的单调性极值与最值、证明不等式,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
若函数f(x)=x3-bx,(b∈R)在区间(1,2)上有零点,则b的取值范围是( )
| A、(4,+∞) |
| B、(1,4) |
| C、(-4,-1) |
| D、(-∞,1) |
直线xsinα+y-5=0的倾斜角的范围是( )
| A、[0,π) | ||||||||||||
B、[
| ||||||||||||
C、[0,
| ||||||||||||
D、[
|
已知抛物线方程为y2=8x,直线l的方程为x-y+2=0,在抛物线上有一动点P到y轴距离为d1,P到l的距离为d2,则d1+d2的最小值为( )
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|