题目内容
18.对于定义域为R的函数f(x),若存在非零实数x0,使函数f(x)在(-∞,x0)和(x0,+∞)上与x轴均有交点,则称x0为函数f(x)的一个“界点”.则下列四个函数中,不存在“界点”的是( )| A. | f(x)=x2+bx-2(b∈R) | B. | f(x)=|x2-3| | C. | f(x)=1-|x-2| | D. | f(x)=x3+x |
分析 理解题意,明确界点的含义,对于各个函数逐一判定.
解答 解:根据题意,
A.f(x)=x2+bx-2(b∈R),判别式恒大于0,有“界点”.
B.f(x)=|x2-3|于x=$\sqrt{3}$,x=-$\sqrt{3}$相等,因此可知存在“界点”成立,
C.f(x)=1-|x-2|=0,解得x=3或x=1,因此可知存在“界点”成立
D.f(x)=x3+x=0,解得x=0,或x=1,故不存在“界点.
故选:D.
点评 本题主要考察函数单调性的判断,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在复平面内,复数2-i(i是虚数单位)的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.执行如图的程序框图,则输出S的值为( )
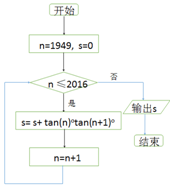

| A. | $\frac{tan2017°-tan1949°}{tan1°}$-67 | B. | $\frac{tan2016°-tan1949°}{tan1°}$-67 | ||
| C. | $\frac{tan2017°-tan1949°}{tan1°}$-68 | D. | $\frac{tan2016°-tan1949°}{tan1°}$-68 |
7.在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
(1)利用最小二乘法求y对x的回归直线方程;
(2)预测所挂物体重量为8g时的弹簧长度.
(参考公式及数据:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}},a=\overline y-b\overline x$,$\sum_{i=1}^5{{x_i}^2}=55$$\sum_{i=1}^5{{x_i}{y_i}}=72$)
| 物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
(2)预测所挂物体重量为8g时的弹簧长度.
(参考公式及数据:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}},a=\overline y-b\overline x$,$\sum_{i=1}^5{{x_i}^2}=55$$\sum_{i=1}^5{{x_i}{y_i}}=72$)