题目内容
如图分别是正三棱台ABC-A1B1C1的直观图和正视图，O，O1分别是上下底面的中心，E是BC中点．
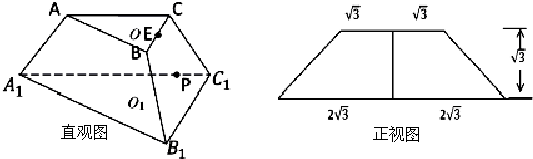
（1）求正三棱台ABC-A1B1C1的体积；（注：棱台体积公式：V=
（S上+
+S下）h，其中s上为棱台上底面面积，s下为棱台下底面面积，h为棱台高）
（2）求平面EA1B1与平面A1B1C1的夹角的余弦；
（3）若P是棱A1C1上一点，求CP+PB1的最小值．
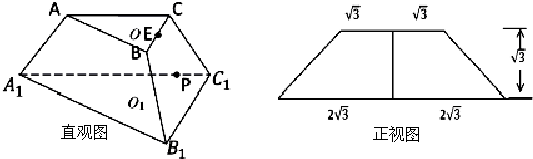
（1）求正三棱台ABC-A1B1C1的体积；（注：棱台体积公式：V=
| 1 |
| 3 |
| S上•S下 |
（2）求平面EA1B1与平面A1B1C1的夹角的余弦；
（3）若P是棱A1C1上一点，求CP+PB1的最小值．
考点：棱柱、棱锥、棱台的体积
专题：综合题,空间位置关系与距离,空间角
分析：（1）利用V=
（S上+
+S下）h，求正三棱台ABC-A1B1C1的体积；
（2）设O，O1分别是上下底面的中心，E是BC中点，F是B1C1中点．以O1为原点，过O1平行B1C1的线为x轴建立空间直角坐标系O1-xyz，利用向量的夹角公式即可求解；
（3）利用展开图，结合余弦定理求CP+PB1的最小值．
| 1 |
| 3 |
| S上•S下 |
（2）设O，O1分别是上下底面的中心，E是BC中点，F是B1C1中点．以O1为原点，过O1平行B1C1的线为x轴建立空间直角坐标系O1-xyz，利用向量的夹角公式即可求解；
（3）利用展开图，结合余弦定理求CP+PB1的最小值．
解答：
解：（1）由题意，AC=2
，A1C1=4
，正三棱台高为
，
∴S上=3
，S下=12
，
∴V=
（S上+
+S下）h=21；
（2）设O，O1分别是上下底面的中心，E是BC中点，F是B1C1中点．以O1为原点，过O1平行B1C1的线为x轴建立空间直角坐标系O1-xyz．C1（-2
，2，0），C（-
，1，
），E（0，1，
），A1（0，-4，0），B1（2
，2，0），
∴
=（0，1，
），
=（2
，6，0），
设平面EA1B1的一个法向量
=（x，y，z），则
取
=（-3，
，-5），取平面A1B1C1的一个法向量
=（0，0，1），设所求角为θ，则cosθ=
；
（3）将梯形A1ACC1绕A1C1旋转到A1A′C′C1，使其与△A1B1C1成平角，
cos∠C′C1A1=cos∠CC1A1=
，sin∠CC1A1=
，
∴cos∠CC1B1=cos（∠CC1A1+
）=-
，
△C′C1B1中，C′C1=
，C1B1=4
，
由余弦定理得C′B1=
，即CP+PB1的最小值为
．
| 3 |
| 3 |
| 3 |
∴S上=3
| 3 |
| 3 |
∴V=
| 1 |
| 3 |
| S上•S下 |
（2）设O，O1分别是上下底面的中心，E是BC中点，F是B1C1中点．以O1为原点，过O1平行B1C1的线为x轴建立空间直角坐标系O1-xyz．C1（-2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∴
| A1E |
| 3 |
| A1B1 |
| 3 |
设平面EA1B1的一个法向量
| n |
|
取
| n |
| 3 |
| m |
5
| ||
| 37 |
（3）将梯形A1ACC1绕A1C1旋转到A1A′C′C1，使其与△A1B1C1成平角，
cos∠C′C1A1=cos∠CC1A1=
| ||
| 7 |
2
| ||
| 7 |
∴cos∠CC1B1=cos（∠CC1A1+
| π |
| 3 |
| ||
| 14 |
△C′C1B1中，C′C1=
| 3 |
| 3 |
由余弦定理得C′B1=
| 67 |
| 67 |
点评：本题考查正三棱台ABC-A1B1C1的体积，考查平面EA1B1与平面A1B1C1的夹角的余弦，考查侧面展开图的运用，考查学生推理论证的能力，属于中档题．
练习册系列答案
相关题目
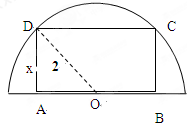如图，有一块半径为2的半圆形钢板，计划剪裁成矩形ABCD的形状，设AD=x，矩形ABCD的面积为y，
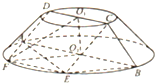如图所示，圆台上、下底面半径分别为4，8，母线与底面所成角为45°，平面ABCD为圆台的轴截面，E为下底面圆弧上一点，且∠ABE=60°，过CDE的平面交⊙O2于点F．