题目内容
11.若复数$\frac{1+ai}{2-i}$(a∈R)的实部和虚部相等,则实数a的值为( )| A. | 1 | B. | -1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
分析 利用复数的运算法则、实部和虚部的定义即可得出.
解答 解:复数$\frac{1+ai}{2-i}$=$\frac{(1+ai)(2+i)}{(2-i)(2+i)}$=$\frac{2-a}{5}$+$\frac{(1+2a)}{2}i$的实部和虚部相等,
∴$\frac{2-a}{5}$=$\frac{1+2a}{5}$,解得a=$\frac{1}{3}$.
故选:C.
点评 本题考查了复数的运算法则、实部和虚部的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
3.不等式x2-4x+3<0的解集为( )
| A. | (1,3) | B. | (-3,-1) | C. | (-∞,-3)∪(-1,+∞) | D. | (-∞,1)∪(3,+∞) |
19.已知偶函数f(x)的定义域为R,且f(1+x)=f(1-x),当0≤x≤1时,f(x)=3x-1;若关于x的方程$f(x)-{log_m}\frac{1}{x+2}=0$在x∈[0,5]上有4个不相等的实数根,则实数m的取值范围是( )
| A. | $(0\;,\;\frac{{\sqrt{7}}}{7})$ | B. | $(\frac{{\sqrt{7}}}{7}\;,\;1)$ | C. | $(\frac{{\sqrt{5}}}{5}\;,\;1)$ | D. | $(\frac{{\sqrt{7}}}{7}\;,\;\frac{{\sqrt{5}}}{5})$ |
20.为了得到函数$y=cos(2x-\frac{π}{2})$的图象,可以将函数y=cos2x的图象( )
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向左平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
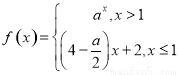 是R上的单调递增函数,则实数a的取值范围为( )
是R上的单调递增函数,则实数a的取值范围为( ) 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为16.
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为16.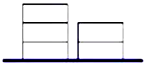 如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).
如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).