题目内容
13.在△ABC中,已知三个内角为A,B,C满足sinA:sinB:sinC=6:5:4,则sinB=( )| A. | $\frac{{\sqrt{7}}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{{5\sqrt{7}}}{16}$ | D. | $\frac{9}{16}$ |
分析 利用正弦定理余弦定理即可得出.
解答 解:∵sinA:sinB:sinC=6:5:4,∴a:b:c=6:5:4,
不妨取a=6,b=5,c=4.
则cosB=$\frac{{6}^{2}+{4}^{2}-{5}^{2}}{2×6×4}$=$\frac{9}{16}$,B∈(0,π).
则sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{5\sqrt{7}}{16}$.
故选:C.
点评 本题考查了正弦定理余弦定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.某几何体的三视图如图所示,则该几何体的体积为( )
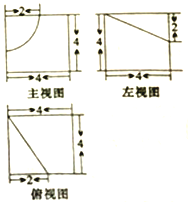

| A. | 64 | B. | 64-4π | C. | 64-8π | D. | 64-$\frac{4π}{3}$ |
5.化简sin2(2π-α)+cos(π+α)cos(π-α)+1( )
| A. | 0 | B. | 2sin2α+1 | C. | 2cos2α+1 | D. | 2 |
3.已知;$f(n)=\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$,则f(n+1)-f(n)=( )
| A. | $\frac{1}{2n+1}+\frac{1}{2n+2}$ | B. | $\frac{1}{2n+2}-\frac{1}{n+1}$ | ||
| C. | $\frac{1}{2n+2}$ | D. | $\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}$ |