题目内容
6.若f(x)是定义域为R,最小正周期$\frac{3π}{2}$的函数,若f(x)=sinx,x∈[0,π],则f($\frac{15π}{4}$)=$\frac{\sqrt{2}}{2}$.分析 根据函数的周期性进行转化求解即可.
解答 解:∵函数的最小正周期$\frac{3π}{2}$,
∴f($\frac{15π}{4}$)=f($\frac{15π}{4}$-$\frac{3π}{2}$×2)=f($\frac{3π}{4}$),
∵f(x)=sinx,x∈[0,π],
∴f($\frac{3π}{4}$)=sin$\frac{3π}{4}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$
点评 本题主要考查函数值的计算,根据函数的周期性进行转化是解决本题的关键.

练习册系列答案
相关题目
16.已知角α的终边经过点P(4,-3),则sinα+2cosα的值等于( )
| A. | $-\frac{3}{5}$ | B. | $-\frac{2}{5}$ | C. | 1 | D. | $\frac{4}{5}$ |
14.双曲线$\frac{x^2}{16}-\frac{y^2}{8}=1$的虚轴长是( )
| A. | 2 | B. | $4\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 8 |
15.命题“若 $α=\frac{π}{4}$,则 tanα=1”的逆否命题是( )
| A. | 若 $α≠\frac{π}{4}$,则tanα≠1 | B. | 若 $α=\frac{π}{4}$,则tanα≠1 | ||
| C. | 若 tanα≠1,则$α≠\frac{π}{4}$ | D. | 若 tanα≠1,则$α=\frac{π}{4}$ |
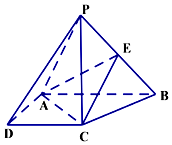 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.