题目内容

下列各式：
①（log23）2=2log23；
②log232=2log23；
③log26+log23=log218；
④log26-log23=log23．
其中正确的有（　　）
A、1个B、2个C、3个D、4个
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数的运算性质和运算法则求解．
解答： 解：①（log23）2≠2log23=log232，故①错误；
②log232=2log23，故②正确；
③log26+log23=log218，故③正确；
④log26-log23=log22≠log23，故④错误．
故选：B．
点评：本题考查命题真假的判断，是基础题，解题时要熟练掌握对数的运算性质和运算法则．
练习册系列答案
相关题目
已知函数f（x）的定义域为（-1，1），2f（x）=f（-x）+x，则f（x）=
 
．
用秦九韶算法求多项式f（x）=7x7+6x6+5x5+4x4+3x3+2x2+x，当x=3时的值为
 
．
数列{an}的通项公式为an=nsin
nπ
2
+1，Sn为其前n项的和，则S2013=
 
．
已知平面α内有两定点A，B，|AB|=3，M，N在α的同侧且MA⊥α，NB⊥α，|MA|=1，|NB|=2，在α上的动点P满足PM，PN与平面α所成的角相等，则点P的轨迹所包围的图形的面积等于（　　）
A、9πB、8πC、4πD、π
函数y=|sinx|（-
π
2
＜x＜
π
2
）的大致图象是（　　）
A、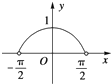
B、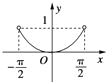
C、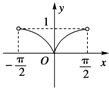
D、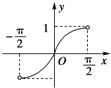
6本不同的书分给甲、乙、丙三人，每人两本，不同的分法种数是（　　）
A、
C
2
6
C
2
4
C
2
2
B、
C
2
6
C
2
4
C
2
2
A
 
3
3
C、6A
 
3
3
D、C
 
3
6
若a＞b，c＞d且c+d＜0，则下列不等式一定成立的是（　　）
A、ac＞bc
B、ac＜bc
C、ad＞bd
D、ad＜bd
设有两个集合A={a，b，c，d，e}，B={f，g}，则集合A到集合B的映射的个数有（　　）
A、10B、25C、32D、20

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网