题目内容
15.记max{a,b}表示a,b中较大的数,则函数f(x)=x•max{-$\frac{lnx}{ln2}$,4x2}(x>0)的递增区间为( )| A. | (0,e) | B. | (0,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$),($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$),(e,+∞) |
分析 根据题意,画出函数y=-$\frac{lnx}{ln2}$与y=4x2(x>0)的图象,结合图象得出函数y=-$\frac{lnx}{ln2}$与y=4x2(x>0)的图象交于点($\frac{1}{2}$,1);由此得出函数f(x)的一个增区间是($\frac{1}{2}$,+∞),再求出f(x)另一个增区间即可.
解答 解:根据题意,画出函数y=-$\frac{lnx}{ln2}$与y=4x2(x>0)的图象如图所示;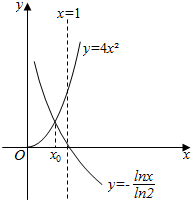
函数y=-$\frac{lnx}{ln2}$是单调减函数,且交x轴与点(1,0),
y=4x2(x>0)是增函数,且过原点;
则函数y=-$\frac{lnx}{ln2}$与y=4x2(x>0)的图象交于点($\frac{1}{2}$,1);
∴当x>$\frac{1}{2}$时,-$\frac{lnx}{ln2}$<4x2(x>0),
此时函数f(x)=x•max{-$\frac{lnx}{ln2}$,4x2}=4x3是增函数,
对应的区间($\frac{1}{2}$,+∞)是增区间;
当x∈(0,$\frac{1}{2}$)时,f(x)=x•max{-$\frac{lnx}{ln2}$,4x2}=-$\frac{xlnx}{ln2}$,
f′(x)=-$\frac{lnx+1}{ln2}$,
∴当0<x<$\frac{1}{e}$时,f′(x)>0,f(x)是增函数,
$\frac{1}{e}$<x<$\frac{1}{2}$时,f′(x)<0,f(x)是减函数;
综上,f(x)的单调增区间是(0,$\frac{1}{e}$)与($\frac{1}{2}$,+∞).
故选:C.
点评 本题考查了新定义的函数的单调性判断问题,解题时应根据题意画出图象,结合图象解答问题,是综合题.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案| A. | 直线x-y=0上 | B. | 直线2x-y-1=0右下方的区域内 | ||
| C. | 直线x+y-8=0左下方的区域内 | D. | 直线x-y+2=0左上方的区域内 |
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
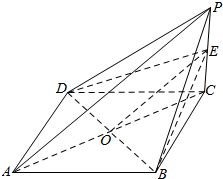 如图所示,在四棱锥P-ABCD中,四边形ABCD是边长为2的正方形,平面ABCD⊥平面PCD,∠PCD=90°,PC=1.5,E是侧棱PC上的动点.
如图所示,在四棱锥P-ABCD中,四边形ABCD是边长为2的正方形,平面ABCD⊥平面PCD,∠PCD=90°,PC=1.5,E是侧棱PC上的动点.