题目内容
12.若函数f(x)的定义域是{x|0<x≤1},求f(cosα)的定义域.分析 函数f(x)的定义域是{x|0<x≤1},可得0<cosα≤1,解出即可得出:f(cosα)的定义域.
解答 解:∵函数f(x)的定义域是{x|0<x≤1},
∴0<cosα≤1,
解得$2kπ-\frac{π}{2}$<α<$\frac{π}{2}$+2kπ,k∈Z.
∴f(cosα)的定义域为($2kπ-\frac{π}{2}$,$\frac{π}{2}$+2kπ),k∈Z.
点评 本题考查了函数的定义域、三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
7.若函数f(x)=1+$\frac{a}{{a}^{x}-1}$是奇函数,则a的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
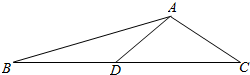 在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD
在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD