题目内容
16.函数$f(x)=\sqrt{-{x^2}+4x+12}$的单调递增区间为[-2,2].分析 根据二次个数的性质以及二次个数的性质求出函数的递增区间即可.
解答 解:令g(x)=-x2+4x+12=-(x-2)2+16,
令g(x)≥0,解得:-2≤x≤6,
而g(x)的对称轴是:x=2,
故g(x)在[-2,2)递增,在(2,6]递减,
故函数f(x)在[-2,2]递增,
故答案为:[-2,2].
点评 本题考查了二次函数的性质,考查函数的单调性问题,是一道基础题.

练习册系列答案
相关题目
6.若10x=3,10y=4,则10x+y的值为( )
| A. | 700 | B. | 300 | C. | 400 | D. | 12 |
4.从长方体一个顶点出发的三条棱长分别为2、3、4,则其对角线的长为( )
| A. | 3 | B. | 5 | C. | $\sqrt{26}$ | D. | $\sqrt{29}$ |
11.某人通过普通话二级测试的概率是$\frac{1}{3}$,他连线测试3次,那么其中恰有1次通过的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{27}$ | D. | $\frac{2}{9}$ |
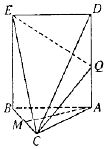 如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点
如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点