题目内容
8.设函数f(x)=logax(a>0且a≠1),若f(x1x2…x2017)=8,则f(x12)+f(x22)+…+f(x20172)的值等于( )| A. | 2loga8 | B. | 16 | C. | 8 | D. | 4 |
分析 根据对数的运算性质,f(x1x2…x2017)=8,可得,f(x12)+f(x22)+…+f(x20172)=f[(x1x2…x2017)]2可得答案.
解答 解:函数f(x)=logax(a>0且a≠1),
∵f(x1x2…x2017)=8,即f(x1)+f(x2)+…+f(x2017)=logax1+logax22+…+logax2017=8
∵f(x2)=logax2=2logax
那么:f(x12)+f(x22)+…+f(x20172)=2[f(x1)+f(x2)+…+f(x2017)]=2×8=16.
故选:B
点评 本题主要考查了对数的运算性质的运用,属于基础题.

练习册系列答案
相关题目
18.已知cosα=$-\frac{5}{13}$,角α是第二象限角,则tan(2π-α)等于( )
| A. | $\frac{12}{13}$ | B. | -$\frac{12}{13}$ | C. | $\frac{12}{5}$ | D. | -$\frac{12}{5}$ |
3.如果集合A={x|x>-1},那么( )
| A. | 0⊆A | B. | {0}∈A | C. | ∅∈A | D. | {0}⊆A |
20.过点$P(2\sqrt{3},3)$且倾斜角为30o的直线方程为( )
| A. | .$y+4\sqrt{3}=3x$ | B. | .$y=x-\sqrt{3}$ | C. | $3y-3=\sqrt{3}x$ | D. | .$y-\sqrt{3}=\sqrt{3}x$ |
18.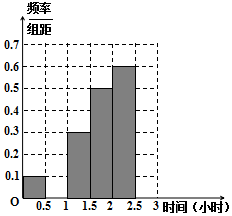 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.
(Ⅰ)确定x,y,p,q的值,并补全频率分布直方图;
(Ⅱ)为进一步了解使用微信对自己的日常工作和生活是否有影响,从“非微信达人”和“微信达人”60人中用分层抽样的方法确定5人,若需从这5人中随机选取2人进行问卷调查,求选取的2人中恰有1人为“微信达人”的概率.
 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过两小时的人被定义为“非微信达人”.已知“非微信达人”与“微信达人”人数比恰为3:2.(Ⅰ)确定x,y,p,q的值,并补全频率分布直方图;
(Ⅱ)为进一步了解使用微信对自己的日常工作和生活是否有影响,从“非微信达人”和“微信达人”60人中用分层抽样的方法确定5人,若需从这5人中随机选取2人进行问卷调查,求选取的2人中恰有1人为“微信达人”的概率.
| 使用微信时间 (单位:小时) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |