题目内容
已知点A(-1,0),B(1,0),P是平面上一动点,且满足|
|•|
|=
•
.
(Ⅰ)设点P的轨迹为曲线C,求曲线C的方程;
(Ⅱ)M是曲线C上的动点,以线段MB为直径作圆,证明该圆与y轴相切;
(Ⅲ)已知点Q(m,2)在曲线C上,过点Q引曲线C的两条动弦QD和QE,且QD⊥QE.判断:直线DE是否过定点?试证明你的结论.
| PB |
| AB |
| PA |
| BA |
(Ⅰ)设点P的轨迹为曲线C,求曲线C的方程;
(Ⅱ)M是曲线C上的动点,以线段MB为直径作圆,证明该圆与y轴相切;
(Ⅲ)已知点Q(m,2)在曲线C上,过点Q引曲线C的两条动弦QD和QE,且QD⊥QE.判断:直线DE是否过定点?试证明你的结论.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设P(x,y),代入|
|•|
|=
•
,能求出曲线C的方程.
(Ⅱ)设M(x,y),则由抛物线的定义知圆的通径为x=1,由已知条件推导出圆心坐标为(
,
),由此能证明直线与圆相切.
(Ⅲ)由已知条件分别求出D(
-
+1,
-2),E(4k2+4k+1,-4k-2),从而得到直线DE的方程为y+2=
(x-5),由此求出直线DE过定点(5,-2).
| PB |
| AB |
| PA |
| BA |
(Ⅱ)设M(x,y),则由抛物线的定义知圆的通径为x=1,由已知条件推导出圆心坐标为(
| x+1 |
| 2 |
| y |
| 2 |
(Ⅲ)由已知条件分别求出D(
| 4 |
| k2 |
| 4 |
| k |
| 4 |
| k |
| k |
| -k2-k+1 |
解答:
(Ⅰ)解:设P(x,y),代入|
|•|
|=
•
,
得
=1+x,
化简,得y2=4x.
∴曲线C的方程为y2=4x.(4分)
(Ⅱ)证明:设M(x,y),则由抛物线的定义知圆的通径为x=1,
∵圆心为线段MB的中点,且B(1,0),
∴圆心坐标为(
,
),
∴圆心到y轴的距离等于半径,
∴直线与圆相切.(8分)
(Ⅲ)解:将Q(m,2)代入y2=4x,得m=1,∴点Q的坐标为(1,2),
设直线QD的方程为y-2=k(x-1),代入y2=4x,得y2-
y+
-4=0,
由y1=2,得y2=
-2,
∴D(
-
+1,
-2),
同理可设QE:y-2=-
(x-1),代入y2=4x,得E(4k2+4k+1,-4k-2),
由此直线DE的方程为:y+4k+2=
(x-4k2-4k-1),
化简,得(-k2-k+1)y=kx+2k2-3k-2,
即y+2=
(x-5),
∴直线DE过定点(5,-2).(13分)
| PB |
| AB |
| PA |
| BA |
得
| (x-1)2+y2 |
化简,得y2=4x.
∴曲线C的方程为y2=4x.(4分)
(Ⅱ)证明:设M(x,y),则由抛物线的定义知圆的通径为x=1,
∵圆心为线段MB的中点,且B(1,0),
∴圆心坐标为(
| x+1 |
| 2 |
| y |
| 2 |
∴圆心到y轴的距离等于半径,
∴直线与圆相切.(8分)
(Ⅲ)解:将Q(m,2)代入y2=4x,得m=1,∴点Q的坐标为(1,2),
设直线QD的方程为y-2=k(x-1),代入y2=4x,得y2-
| 4 |
| k |
| 8 |
| k |
由y1=2,得y2=
| 4 |
| k |
∴D(
| 4 |
| k2 |
| 4 |
| k |
| 4 |
| k |
同理可设QE:y-2=-
| 1 |
| k |
由此直线DE的方程为:y+4k+2=
| ||||
|
化简,得(-k2-k+1)y=kx+2k2-3k-2,
即y+2=
| k |
| -k2-k+1 |
∴直线DE过定点(5,-2).(13分)
点评:本题考查曲线方程的求法,考查直线与圆相切的证明,考查直线是否过定点的判断与证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
如图是导函数y=f′(x)的图象,那么函数y=f(x)在下面哪个区间是减函数( )
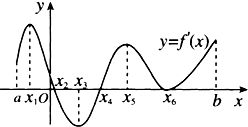

| A、(x1,x3) |
| B、(x2,x4) |
| C、(x4,x6) |
| D、(x5,x6) |
执行所示的程序框图,如果输入N=5,则输出的数等于( )
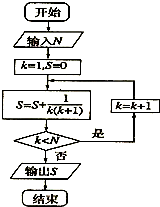

A、
| ||
B、
| ||
C、
| ||
D、
|

 平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.
平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2. 已知抛物线x2=4y,直线l:y=x-2,F是抛物线的焦点.
已知抛物线x2=4y,直线l:y=x-2,F是抛物线的焦点.