Question

17．已知f（x）=2^x-x²共有m个零点，g（x）=2^x+x²-2有n个零点，且f（x）=2^x-x²的一个零点为4，则m+n=5．

Answer 1

分析 f（x）=2^x-x²的零点的个数可化为y=2^x与y=x²的图象的交点的个数，g（x）=2^x+x²-2的零点的个数可化为y=2^x与y=2-x²的图象的交点的个数，作图象求解即可．

解答 解：f（x）=2^x-x²的零点的个数可化为y=2^x与y=x²的图象的交点的个数，
g（x）=2^x+x²-2的零点的个数可化为y=2^x与y=2-x²的图象的交点的个数，
作函数y=2^x、y=2-x²与y=x²的图象如下，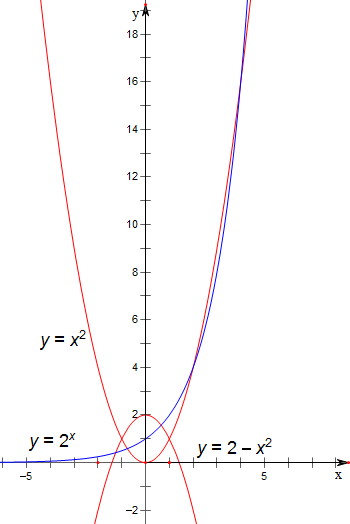

由图象可知，
y=2^x与y=x²的图象有三个交点，
y=2^x与y=2-x²的图象有两个交点，
故m=3，n=2，
故答案为：5．

点评 本题考查了函数的图象的作法及数形结合的思想应用．