题目内容
17.将二项式${(x+\frac{2}{{\sqrt{x}}})^6}$展开式各项重新排列,则其中无理项互不相邻的概率是( )| A. | $\frac{2}{7}$ | B. | $\frac{1}{35}$ | C. | $\frac{8}{35}$ | D. | $\frac{7}{24}$ |
分析 首先由二项式定理求出有理项和无理项的项数,然后利用插空法求出排列数,利用古典概型的公式求概率即可.
解答 解:二项式${(x+\frac{2}{{\sqrt{x}}})^6}$展开式通项为:${T}_{r+1}={C}_{6}^{r}{x}^{6-r}(\frac{2}{\sqrt{x}})^{r}={2}^{r}{C}_{6}^{r}{x}^{6-\frac{3}{2}r}$,知当r=0,2,4,6时为有理项,则二项式${(x+\frac{2}{{\sqrt{x}}})^6}$展开式中有4项有理项,3项无理项,所以基本事件总数为${A}_{7}^{7}$,无理项互为相邻有${A}_{4}^{4}{A}_{5}^{3}$,所以所求概率P=$\frac{{A}_{4}^{4}{A}_{5}^{3}}{{A}_{7}^{7}}=\frac{2}{7}$,
故选:A.
点评 本题考查了二项式定理以及插空法求排列数、古典概型的概率求法;属于中档题.

练习册系列答案
相关题目
8.某几何体的三视图如图所示,则该几何体的体积是( )
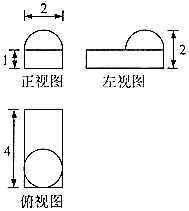

| A. | 8+$\frac{4}{3}$π | B. | 8+$\frac{2}{3}$π | C. | 4+$\frac{4π}{3}$ | D. | 4+$\frac{2π}{3}$ |
12.定义R上的减函数f(x),其导函数f'(x)满足$\frac{f(x)}{f'(x)}<1-x$,则下列结论正确的是( )
| A. | 当且仅当x∈(-∞,1),f(x)<0 | B. | 当且仅当x∈(1,+∞),f(x)>0 | ||
| C. | 对于?x∈R,f(x)<0 | D. | 对于?x∈R,f(x)>0 |
2.已知F是抛物线C:y=2x2的焦点,点P(x,y)在抛物线C上,且x=1,则|PF|=( )
| A. | $\frac{9}{8}$ | B. | $\frac{3}{2}$ | C. | $\frac{17}{8}$ | D. | $\frac{5}{2}$ |
1.设a,b,c大于0,则3个数$\frac{a}{b},\frac{b}{c},\frac{c}{a}$的值( )
| A. | 至多有一个不大于1 | B. | 都大于1 | ||
| C. | 至少有一个不大于1 | D. | 都小于1 |
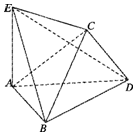 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.