题目内容
11．在空间，下列条件可以确定一个平面的是（ ）| A． | 两条直线 | B． | 一点和一条直线 | C． | 一个三角形 | D． | 三个点 |
分析 在A中，两条异面直线不能确定一个平面；在B中，若点在直线上，由不能确定一个平面；在C中，一个三角形确定一个平面；在D中，如果共点共线，不能确定一个平面．
解答 解：在A中，两条相交线和两条平行线都能确定一个平面，
但两条异面直线不能确定一个平面，故A错误；
在B中，直线与直线外一点确定一个平面，
若点在直线上，由不能确定一个平面，故B错误；
在C中，因为一个三角形的三个顶点不共线，所以一个三角形确定一个平面，故C正确；
在D中，不共线的三点确定一个平面，如果共点共线，不能确定一个平面，故D错误．
故选：C．
点评 本题考查能确定一个平面的充要条件的判断，是基础题，解题时要认真审题，注意平面的基本性质及推论的合理运用．
练习册系列答案
相关题目
12．已知等差数列{an}中，a2，a8是函数f（x）=x2-3x+5的两个零点．则a1+a9的值为（ ）
| A． | -3 | B． | 5 | C． | 3 | D． | -5 |
16．
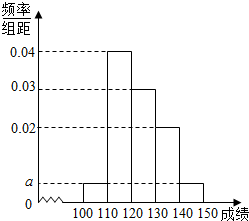贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示，其中成绩分组区间是[100，110），[110，120），[120，130），[130，140），[140，150]．
（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生数学成绩的平均分；
（Ⅲ）若这100名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[100，140）之外的人数．
贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示，其中成绩分组区间是[100，110），[110，120），[120，130），[130，140），[140，150]．（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生数学成绩的平均分；
（Ⅲ）若这100名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[100，140）之外的人数．
| 分数段 | [100，110） | [110，120） | [120，130） | [130，140） |
| x：y | 1：1 | 2：1 | 3：4 | 4：5 |
3．函数$f（x）=sin（x+\frac{π}{6}）cos（x+\frac{π}{6}）$，给出下列结论正确的是（ ）
| A． | f（x）的最小正周期为 $\frac{π}{2}$ | B． | f（x）的一条对称轴为$x=\frac{π}{6}$ | ||
| C． | f（x）的一个对称中心为$（\frac{π}{6}，0）$ | D． | $f（x-\frac{π}{6}）$是奇函数 |
