题目内容
8.给出下列四个结论:①已知直线l1:ax+y+1=0,l2:x+ay+a2=0,则l1∥l2的充要条件为a=±1;
②函数f(x)=$\sqrt{3}$sinωx+cosωx满足f(x+$\frac{π}{2}$)=-f(x),则函数f(x)的一个对称中心为($\frac{π}{6}$,0);
③已知平面α和两条不同的直线a,b,满足b?α,a∥b,则a∥α;
④函数f(x)=$\frac{1}{x}$+lnx的单调区间为(0,1)∪(1,+∞).
其中正确命题的个数为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 0 |
分析 根据直线平行判断①,根据三角函数的性质判断②,根据线面平行判断③,根据导数的应用判断④.
解答 解:对于①,由l1∥l2,得$\left\{\begin{array}{l}{{a}^{2}-1=0}\\{{a}^{2}-a≠0}\end{array}\right.$,
解得:a=-1,①错;
对于②,由f(x+$\frac{π}{2}$)=-f(x),得:f(x+π)=f(x),
∴f(x)的周期是π,ω=2,
∴f(x)=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$),
故x=$\frac{π}{6}$时,f(x)=2,②错;
对于③,a?α时,结论不成立,③错;
对于④,f(x)=$\frac{1}{x}$+lnx,f(x)的定义域是(0,+∞),
f′(x)=$\frac{x-1}{{x}^{2}}$,由f′(x)>0,得:x>1,
由f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减,在(1,+∞)递增,④错;
故选:D.
点评 本题考查了充分必要条件,考查三角函数,直线的平行的关系以及导数的应用,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知sinθ+cosθ=2sinα,sin2θ=2sin2β,则( )
| A. | cosβ=2cosα | B. | cos2β=2cos2α | C. | cos2β+2cos2α=0 | D. | cos2β=2cos2α |
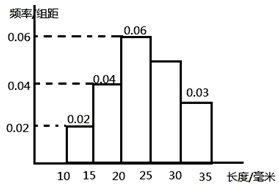 对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;
对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;