题目内容
13.已知曲线$\frac{y^2}{b}$-$\frac{x^2}{a}$=1(a•b≠0且a≠b)与直线x+y-2=0相交于P,Q两点,且$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0(O为原点),则$\frac{1}{b}$-$\frac{1}{a}$的值为$\frac{1}{2}$.分析 先设p(x1,y1);Q(x2,y2),根据题设条件kop*koq=-1即;y1y2=-x1x2直线方程与双曲线方程联立,求得x1+x2=和x1x2的表达式,代入y1y2=-x1x2求得答案.
解答 解:设p(x1,y1),Q(x2,y2),
∵$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,
∴kop*koq=-1即;y1y2=-x1x2
联立直线x+y-2=0和曲线$\frac{y^2}{b}$-$\frac{x^2}{a}$=1两方程可得:(a-b)x2-4ax+4a-ab=0,
x1+x2=$\frac{4a}{a-b}$,x1x2=$\frac{4a-ab}{a-b}$,
y1y2=(2-x1)(2-x2)=4-2(x1+x2)+x1x2=-x1x2
即4-2•$\frac{4a}{a-b}$+$\frac{4a-ab}{a-b}$=-$\frac{4a-ab}{a-b}$,
即ab=2a-2b,
则$\frac{1}{b}$-$\frac{1}{a}$=$\frac{a-b}{ab}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题主要考查了双曲线的应用.考查了学生综合分析问题的能力,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
3.已知集合A={(x,y)|x2+y2≤4,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为( )
| A. | 49 | B. | 45 | C. | 69 | D. | 73 |
4.已知函数f(x)=$\frac{x+1}{{x}^{2}}$,g(x)=log2x+m,若对?x1∈[1,2],?x2∈[1,4],使得f(x1)≥g(x2),则m的取值范围是( )
| A. | m≤-$\frac{5}{4}$ | B. | m≤2 | C. | m≤$\frac{3}{4}$ | D. | m≤0 |
5.函数f(x)的导函数为f′(x),对?x∈R,都有2f′(x)>f(x)成立,若f(ln4)=2,则不等式f(x)>e${\;}^{\frac{x}{2}}}$的解集是( )
| A. | (1,+∞) | B. | (0,ln4) | C. | (ln4,+∞) | D. | (0,1) |
3.设$f(x)=sin(x+\frac{π}{3});a=f(\frac{π}{12}),b=f(\frac{π}{6}),c=f(\frac{π}{3})$,则( )
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | b>a>c |
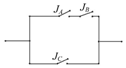 如图,JA,JB两个开关串联再与开关JC并联,在某段时间内每个开关能够闭合的概率都是0.5,计算在这段时间内线路正常工作的概率为0.625.
如图,JA,JB两个开关串联再与开关JC并联,在某段时间内每个开关能够闭合的概率都是0.5,计算在这段时间内线路正常工作的概率为0.625.