题目内容
1.过点(-10,10)且在x轴上截距是在y轴上截距的4倍的直线的方程为( )| A. | x-y=0 | B. | x+4y-30=0 | ||
| C. | x+y=0 或x+4y-30=0 | D. | x+y=0或x-4y-30=0 |
分析 分直线经过原点和直线不经过原点两种情况,分别用两点式、截距式求得直线的方程,综合可得结论.
解答 解:在x轴上截距是在y轴上截距的4倍的直线但它经过原点时,它的方程为$\frac{y-0}{10-0}$=$\frac{x-0}{-10-0}$,即x+y=0.
当它不经过原点时,设它的方程为$\frac{x}{4a}$+$\frac{y}{a}$=1,把点(-10,10)代入可得$\frac{-10}{4a}$+$\frac{10}{a}$=1,求得a=$\frac{15}{2}$,
此时它的方程为$\frac{x}{30}$+$\frac{2y}{15}$=1,即x+4y-30=0.
综上可得,要求的直线方程为x+y=0 或x+4y-30=0,
故选:C.
点评 本题主要考查用两点式、截距式求直线的方程,属于基础题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
12.sin75°sin15°+cos70°cos15°的值为( )
| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
16.在△ABC中已知三边a,b,c满足(a+b+c)(b+c-a)=bc,则∠A=( )
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
3.已知定义在R上的函数f(x)满足f($\sqrt{3}$)=-2,f′(x)>-$\sqrt{3}$,若x∈(0,π),则不等式f(2sinx)≤-4$\sqrt{3}$sin$\frac{x}{2}$cos$\frac{x}{2}$+1的解集( )
| A. | [$\frac{π}{3}$,$\frac{2π}{3}$] | B. | (0,$\frac{π}{3}$] | C. | [$\frac{2π}{3}$,π) | D. | (0,$\frac{π}{3}$]∪[$\frac{2π}{3}$,π) |
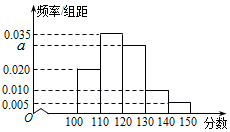 某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.
某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4. 已知正三棱柱ABC-A1B1C1,D为AB上的中点.
已知正三棱柱ABC-A1B1C1,D为AB上的中点.