题目内容
19．函数f（x）=ln（x+1）-$\frac{2}{{x}^{2}}$的零点所在的大致区间为（ ）| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
分析 根据题意，由函数的解析式计算f（1）、f（2）、f（3）、f（4）的值，结合零点存在定理，即可得到所求区间．
解答 解：根据题意，对于函数函数f（x）=ln（x+1）-$\frac{2}{{x}^{2}}$，其定义域为（-1，0）∪（0，+∞），
f（0）不存在，
f（1）=ln2-$\frac{2}{1}$=ln2-1＜0，
f（2）=ln3-$\frac{2}{4}$=ln2-$\frac{1}{2}$＞0，
f（3）=ln4-$\frac{2}{9}$＞0，
f（4）=ln5-$\frac{2}{25}$＞0，
由零点存在定理可得，函数f（x）=ln（x+1）-$\frac{2}{{x}^{2}}$的零点所在的大致区间为（1，2）；
故选：B．
点评 本题考查二分法的运用，本题解题的关键是求出区间的两个端点的函数值，进行比较．
练习册系列答案
阅读快车系列答案
相关题目
随着互联网的发展，移动支付（又称手机支付）越来越普遍，某学校兴趣小组为了了解移动支付在大众中的熟知度，对15～65岁的人群随机抽样调查，调查的问题是“你会使用移动支付吗？”其中，回答“会”的共有n个人，把这n个人按照年龄分成5组：第1组[15，25），第2组[25，35），第3组[35，45），第4组[45，55），第5组[55，65），然后绘制成如图所示的频率分布直方图，其中第一组的频数为20．
10．若函数f（x）=2sin（ωx+φ）对任意的x∈R，都有f（$\frac{π}{3}$-x）=f（x）．若函数g（x）=cos（ωx+φ）-1，则g（$\frac{π}{6}$）的值是（ ）
| A． | -2 | B． | -1 | C． | -$\frac{1}{2}$ | D． | 0 |
4．在△ABC中，a，b，c是内角A，B，C所对应边，a=2，b=$\sqrt{2}$，A=$\frac{π}{4}$，则角B=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{6}$或$\frac{5π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{6}$ |
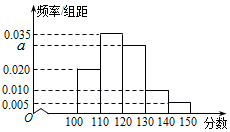某校从高三年级中随机选取200名学生，将他们的一模数学成绩绘制成频率分布直方图（如图）．由图中数据可知a=0.030．若要从成绩在[120，130），[130，140），[140，150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从成绩在[130，140）内的学生中选取的人数应为4．