题目内容
16．已知双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$，它的一个顶点到较近焦点的距离为1，焦点到渐近线的距离是$\sqrt{3}$，则双曲线C的方程为（ ）| A． | x2-$\frac{{y}^{2}}{3}$=1 | B． | $\frac{{x}^{2}}{3}$-y2=1 | C． | $\frac{{x}^{2}}{\sqrt{3}}$-y2=1 | D． | x2-$\frac{{y}^{2}}{9}$=1 |
分析 由题意可得c-a=1，求出渐近线方程和焦点的坐标，运用点到直线的距离公式，可得b=$\sqrt{3}$，由a，b，c的关系，可得a，进而得到所求双曲线的方程．
解答 解：双曲线的一个顶点（a，0）到较近焦点（c，0）的距离为1，
可得c-a=1，
由双曲线的渐近线方程为y=$\frac{b}{a}$x，
则焦点（c，0）到渐近线的距离为d=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=b=$\sqrt{3}$，
又c2-a2=b2=3，
解得a=1，c=2，
即有双曲线的方程为x2-$\frac{{y}^{2}}{3}$=1．
故选：A．
点评 本题考查双曲线的方程的求法，注意运用两点的距离公式和点到直线的距离公式，考查运算能力，属于基础题．
练习册系列答案
相关题目
16．
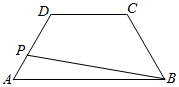如图，在等腰梯形ABCD中，AB=8，BC=4，CD=4，点P在线段AD上运动，则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是（ ）
如图，在等腰梯形ABCD中，AB=8，BC=4，CD=4，点P在线段AD上运动，则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是（ ）| A． | [6，4+4$\sqrt{3}$] | B． | [4$\sqrt{2}$，8] | C． | [4$\sqrt{3}$，8] | D． | [6，12] |
4．已知双曲线C的渐近线方程为3x±2y=0，且焦点在x轴上，焦点到渐近线的距离为6，则该双曲线的方程为（ ）
| A． | $\frac{x^2}{18}-\frac{y^2}{8}=1$ | B． | $\frac{x^2}{36}-\frac{y^2}{16}=1$ | C． | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D． | $\frac{x^2}{16}-\frac{y^2}{36}=1$ |