题目内容
8．已知函数f（x）=$\left\{\begin{array}{l}{-1，x＜-1}\\{x，-1≤x＜1}\\{1，x≥1}\end{array}\right.$（1）求f（x）的定义域；
（2）作出函数f（x）的图象；
（3）根据图象判断函数f（x）的奇偶性．
分析 （1）根据定义域的定义进行求解决即可．
（2）利用分段函数的表达式作出图象即可．
（3）结合函数图象判断函数的对称性进行判断即可．
解答 
解：（1）f（x）的定义域为（-∞，+∞）．
（2）作出函数f（x）的图象如图
（3）由图象知函数关于原点对称，即函数f（x）是奇函数．
点评 本题主要考查函数定义域，函数图象以及函数奇偶性的判断，比较基础．
练习册系列答案
相关题目
16．
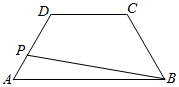如图，在等腰梯形ABCD中，AB=8，BC=4，CD=4，点P在线段AD上运动，则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是（ ）
如图，在等腰梯形ABCD中，AB=8，BC=4，CD=4，点P在线段AD上运动，则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是（ ）| A． | [6，4+4$\sqrt{3}$] | B． | [4$\sqrt{2}$，8] | C． | [4$\sqrt{3}$，8] | D． | [6，12] |
13．已知函数f（x）=$\frac{x-2}{x+2}$，则f（0）=（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | -1 |
20．设函数f1（x）=x2，f2（x）=$\frac{3}{x+1}$，f3（x）=sinπx，xi=$\frac{i}{9}$（i=0，1，2，…，9），记Ik=$\sum_{i=1}^{9}$|fk（xi）-fk（xi-1）|，则（ ）
| A． | I1＜I2＜I3 | B． | I2＜I1＜I3 | C． | I3＜I2＜I1 | D． | I1＜I3＜I2 |