题目内容
4．某单位共有163人，其中老年人27人，中年人55人，青年人81人，为了调查他们的身体状况，需要从他们中抽取一个容量为36的样本，问应当采用怎样的抽样方法？中年人应抽查多少人？分析 由于各部分之间的身体状况有较大差别，故应当采用怎样分层抽样方法，样本才具有可行性．三部分的人数不成比例，应从中年人中随机剔除1人，得：27：54：81=1：2：3，由此能求出中年人应抽查的人数．
解答 解：∵某单位共有163人，其中老年人27人，中年人55人，青年人81人，
为了调查他们的身体状况，需要从他们中抽取一个容量为36的样本，
由于各部分之间的身体状况有较大差别，
∴应当采用怎样分层抽样方法，样本才具有可行性．
∵三部分的人数不成比例，∴应从中年人中随机剔除1人，得：27：54：81=1：2：3，
∴将36人分成1：2：3的三部分，
设三部分各抽取个体数分别为：x，2x，3x，
则x+2x+3x=36，解得x=6，∴2x=12．
故中年人应抽查12人．
点评 本题考查抽查的样本个数的求法，是基础题，解题时要认真审题，注意分层抽样的性质的合理运用．
练习册系列答案
相关题目
9．从某校的一次学料知识竞赛成绩中，随机抽取了50名同学的成绩，统计如下：
（Ⅰ）求这50名同学成绩的样本平均数$\overline{x}$（同一组中的数据用该组区间的中点值作代表）；
（Ⅱ）由频数分布表可以认为，本次学科知识竞赛的成绩Z服从正态分布N（μ，196），其中μ近似为样本平均数$\overline{x}$．
①利用该正态分布．求P（Z＞74）；
②某班级共有20名同学参加此次学科知识比赛，记X表示这20名同学中成绩超过74分的人数，利用①的结果，求EX．附：若Z～N（μ，σ2），则P（μ-σ＜Z＜+σ）=0.6826，P（μ-2＜Z＜μ+2σ）=0.9544．
| 组别 | [30，40] | [40，50] | [50，60] | [60，70] | [70，80] | [80，90] | [90，100] |
| 频数 | 3 | 10 | 12 | 15 | 6 | 2 | 2 |
（Ⅱ）由频数分布表可以认为，本次学科知识竞赛的成绩Z服从正态分布N（μ，196），其中μ近似为样本平均数$\overline{x}$．
①利用该正态分布．求P（Z＞74）；
②某班级共有20名同学参加此次学科知识比赛，记X表示这20名同学中成绩超过74分的人数，利用①的结果，求EX．附：若Z～N（μ，σ2），则P（μ-σ＜Z＜+σ）=0.6826，P（μ-2＜Z＜μ+2σ）=0.9544．
16．
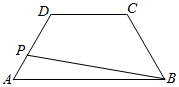如图，在等腰梯形ABCD中，AB=8，BC=4，CD=4，点P在线段AD上运动，则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是（ ）
如图，在等腰梯形ABCD中，AB=8，BC=4，CD=4，点P在线段AD上运动，则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是（ ）| A． | [6，4+4$\sqrt{3}$] | B． | [4$\sqrt{2}$，8] | C． | [4$\sqrt{3}$，8] | D． | [6，12] |
13．已知函数f（x）=$\frac{x-2}{x+2}$，则f（0）=（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | -1 |
4．已知双曲线C的渐近线方程为3x±2y=0，且焦点在x轴上，焦点到渐近线的距离为6，则该双曲线的方程为（ ）
| A． | $\frac{x^2}{18}-\frac{y^2}{8}=1$ | B． | $\frac{x^2}{36}-\frac{y^2}{16}=1$ | C． | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D． | $\frac{x^2}{16}-\frac{y^2}{36}=1$ |