题目内容
如图，已知AB⊥平面α于B，DC?α，且CD⊥AC于C，求证：平面ACD⊥平面ABC．考点：平面与平面垂直的判定
专题：空间位置关系与距离
分析：由AB⊥平面α，CD?α，根据线面垂直的性质可知AB⊥CD，又AC⊥CD，AC∩AB=A，AC?平面ABC，AB?平面ABC，根据线面垂直的判定定理推断出CD⊥平面ABC，进而根据面面垂直的判定定理可推断出平面ACD⊥平面ABC．
解答：
证明：∵AB⊥平面α，CD?α，
∴AB⊥CD，
又AC⊥CD，AC∩AB=A，AC?平面ABC，AB?平面ABC，
∴CD⊥平面ABC，
∵CD?平面ACD，
∴平面ACD⊥平面ABC．
∴AB⊥CD，
又AC⊥CD，AC∩AB=A，AC?平面ABC，AB?平面ABC，
∴CD⊥平面ABC，
∵CD?平面ACD，
∴平面ACD⊥平面ABC．
点评：本题主要考查了面面垂直的判定定理的应用．考查了学生的基础定理的掌握．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
已知点A（0，-3），B（2，3），直线x+4y-1=0过抛物线y=ax2的焦点，动点P在抛物线上，则△PAB面积的最小值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
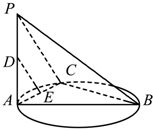如图，已知AB是圆的直径，PA垂直圆所在的平面，C是圆上任一点，D是线段PA的中点，E是线段AC上的一点．
某市居民2009～2013年货币收入x与购买商品支出Y的统计资料如下表所示：