题目内容
已知四个数2，a，b，5成等比数列，则等lgab于（ ）
| A、-1 | B、0 | C、1 | D、2 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：由四个数2，a，b，5 成等比数列，得ab=10，由此能求出lgab的值．
解答：
解：∵四个数2，a，b，5 成等比数列，
∴ab=2×5=10，
∴lgab=lg10=1．
故选：C．
∴ab=2×5=10，
∴lgab=lg10=1．
故选：C．
点评：本题考查对数值的求法，是基础题，解题时要认真审题，注意等比数列的性质的灵活运用．
练习册系列答案
相关题目
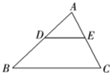如图，已知D、E分别是△ABC的AB、AC边上一点，DE∥BC，且S△ADE：S四边形DBCE=1：3，那么AD：AB等于（ ）A、1：
| ||
| B、1：2 | ||
| C、1：3 | ||
| D、1：4 |
设A1，A2，A3，A4是平面直角坐标系中两两不同的四点，若
=λ
（λ∈R），
=μ
（μ∈R），且
+
=2，则称A3，A4调和分割A1，A2，已知点C（c，0），D（d，0）（c，d∈R）调和分割点A（0，0），B（1，0），则下面说法正确的是（ ）
| A1A3 |
| A1A2 |
| A1A4 |
| A1A2 |
| 1 |
| λ |
| 1 |
| μ |
| A、C可能是线段AB的中点 |
| B、D可能是线段AB的中点 |
| C、C，D可能同时在线段AB上 |
| D、C，D不可能同时在线段AB的延长线上 |
若a＜b＜0，则下列不等式中成立的是（ ）
A、
| ||||
B、b+
| ||||
C、a+
| ||||
D、
|
已知|
|=3，|
|=4，（
+
）•（
+3
）=33，则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
不等式（x-2）（x-1）＜0的解集是（ ）
| A、{x|1＜x＜2} |
| B、{x|x＜1或x＞2} |
| C、{x|x＜1} |
| D、{x|x＞2} |
已知点A（0，-3），B（2，3），直线x+4y-1=0过抛物线y=ax2的焦点，动点P在抛物线上，则△PAB面积的最小值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|