题目内容
6.已知直线$x=\frac{π}{4}\;和\;x=\frac{5π}{4}$是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)图象的两条相邻的对称轴,则φ的值为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
分析 由条件利用正弦函数的图象的周期性求得ω的值,再利用图象的对称性求得φ的值,可得函数的解析式.
解答 解:由题意可得$\frac{5π}{4}$-$\frac{π}{4}$=$\frac{T}{2}$=$\frac{π}{ω}$,∴ω=1,故f(x)=sin(x+φ).
故f($\frac{π}{4}$)=sin($\frac{π}{4}$+φ)=1,f($\frac{5π}{4}$)=sin($\frac{5π}{4}$+φ)=-1 ①;
或 f($\frac{π}{4}$)=sin($\frac{π}{4}$+φ)=-1,f($\frac{5π}{4}$)=sin($\frac{5π}{4}$+φ)=1 ②.
根据0<φ<π,由①求得φ=$\frac{π}{4}$,由②求得 φ无解,
故选:A.
点评 本题主要考查正弦函数的图象的周期性以及图象的对称性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列式子中,正确的是( )
| A. | -1+(-1)=2 | B. | $\frac{1}{2}$+$\frac{1}{3}$=$\frac{1}{5}$ | ||
| C. | 23•2n-1=23n-3 | D. | $\frac{1}{101}$+$\frac{1}{202}$+$\frac{1}{303}$+$\frac{1}{606}$=$\frac{2}{101}$ |

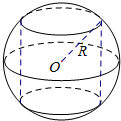 如图所示,半径R=2的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差等于8π.
如图所示,半径R=2的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差等于8π.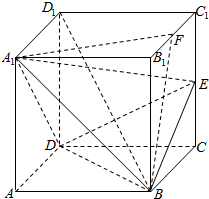 已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.